Complex systems around us

What is the Prisoner’s Dilemma / Social Dilemma?

　The Prisoner’s Dilemma is a kind of game that was devised more than half a century ago. We will explain it using a slightly different story to that used in the original version. (⇒ For the original story, reference “Does cooperation really produce benefits?”)

　The Prisoner’s Dilemma is played by two players. The two are in a situation in which they are unable to confer with each other. This scenario, in which the two players are unable to contact each other, is why the players are referred to as “prisoners.” The players can choose from two alternatives: betray the other player, or cooperate with the other player. However, neither player can know what choice the other player has made. The number of points received by each is dependent on the choices of both players. If A betrays and B cooperates, A gets 5 points. If both cooperate, A gets 3 points. If both betray, A gets 1 point. If A cooperates and B betrays, A gets 0 points. Because the player with the most points is the winner, the players try to earn the highest score.

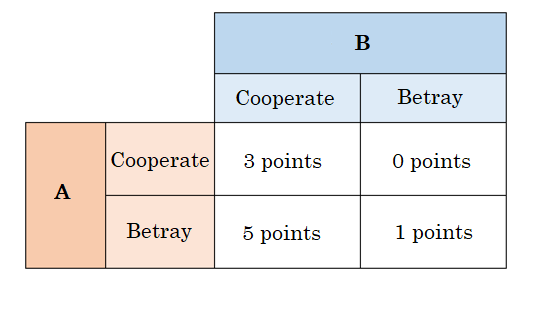
　In what lies the dilemma? In this game, it is impossible to know what choice the other has made. However, the situation is that when A chooses to cooperate, it is better for B to betray (3 points is better than 5 points), and when A chooses to betray, it is also better for B to betray (1 point is better than 0 points). In other words, whatever one player chooses, it is better for the other to betray. This holds true for both players, so both sides betray. When they do that, the outcome is that both players receive 1 point each. Although through cooperation they could win 3 points each, they can only obtain 1 point each, which is why it is called a dilemma. As explained above, the Prisoner’s Dilemma is a game played between two people, but it is easy to expand this to include three or more people under the same conditions. To put it differently, the situation in this game is that whether other people cooperate with you or betray you, you can get more points if you betray others. When that happens, if all players betray the others in order to get more points, the result is that they receive fewer points than they would if they had cooperated with each other. This is called a “Social Dilemma.”

　In other words, the Prisoner’s Dilemma and Social Dilemma consist of the following.

　　・When players act to get high points, they betray each other, with the result that they fail to obtain high points.
　　・When they cooperate with each other they get high points, but if one player betrays the others, he gets more points, which is an inducement to betray.
　　・If not only this player but the other (others) also think the same way and both (all) betray the others, the result is that they end up returning to the starting point (1).

First of all, it is ideal material for social scientists and philosophers considering the nature of humanity（⇒ ＜Reference “The Prisoner’s Dilemma makes us think about human nature”＞). It is also now understood that, even in real-life society, such dilemmas occur with unexpected (?) frequency. (⇒ Reference “Why do people skip the cleaning when it's their turn?”,, “Will eels become extinct as a result of overfishing?” and “Why does doping not disappear?”)

The Prisoner’s Dilemma makes us think about human nature

　The Prisoner’s Dilemma game begins with players not knowing what choice the other has made, but because betrayal produces better outcomes irrespective of what the other player has chosen, even if the other player's choices are known, naturally a player still gets more points for betrayal (⇒ Reference “What is the Prisoner’s Dilemma / Social Dilemma?”). In other words, even if it is known that one has cooperated, it is “rational” behavior for the other to betray them in order to get high points, rather to cooperate. Conversely, it is “irrational” to choose to cooperate for reciprocal (mutual) benefit when the other cooperates.

Does “tit for tat” really lead to a better society?

　In the repeated Prisoner’s Dilemma game, a pattern of behavior known as “tit-for-tat” (“an eye for an eye” behavior) results in high points. (Reference “Prisoner's dilemma tournament.”) How far can this be generalized? To begin with the conclusion, the answer is that it depends on the situation, and on the approach of the other player, but tit-for-tat in a Prisoner’s Dilemma context does, surprisingly, enable players to get high points.

　In addition, tit-for-tat is a “conditioned response” to the other's choice. To put it another way, this pattern of behavior is not based on a “rational” consideration of the other's approach and one's own methods for dealing with it in order to maximize points, nor does it involve difficult calculations (exemplar of reason!) based on past experience and memory (one's own choices and the other's choices). That an intellectual endeavor such as a game could be won by a player acting in accordance with conditioned responses that even a dog could generate (such as those of Pavlov) was another cause for surprise. (Digression: Because it does not require the assumption of rationality, this led to the birth of the field of so-called evolutionary games, which are used to analyze the evolution of behavior in animals - strictly speaking, non-human animals - that are not considered to have the power of reason.)

　The tit-for-tat pattern of behavior achieves decent scores against players using a variety of behavior. For example, it switches to betraying when faced by another player who consistently betrays, so although it gets 0 points in the first round, it wins 1 point after that. Accordingly, tit-for-tat does not induce mutual cooperation. In other words, whether or not society is improved (whether there is mutual cooperation) depends on the other player. 　Now we will modify our ideas somewhat. If we use a pattern of behavior that always cooperates, instead of tit-for-tat, does this really improve society? In fact, that is not necessarily the case. This is where the depth of the Prisoner’s Dilemma / Social Dilemma becomes apparent. (⇒ Reference “Does ‘tit for tat’ really lead to a better society?” and “The Prisoner’s Dilemma makes us think about human nature”)

Does cooperation really produce benefits?

　In the situations known as the Prisoner’s Dilemma / Social Dilemma, although players should cooperate with each other (can get high points), they end up in mutual betrayal. (⇒ Reference “What is the Prisoner’s Dilemma / Social Dilemma?”) For those involved (the players), mutual cooperation may be desirable, but it may be undesirable when viewed from the broadest perspective. Take the example of corruption. Both those paying and receiving bribes avoid scrutiny. Because it is difficult to produce a self-aware victim (it is difficult to find a victim who has been cheated), corruption is exposed by the Special Investigations division of the District Public Prosecutor's Office. It has been emphasized that mutual cooperation is difficult in this dilemma, but there is a system under which the Prisoner’s Dilemma/Social Dilemma is used cleverly against the players, such as by inducing a confession from someone accused of being an accomplice. This really is a Prisoner’s Dilemma. (Actually, it was precisely this story that was used to explain the original situation, which is why it came to be called the Prisoner’s Dilemma.) Plea bargaining is finally scheduled to be introduced in Japan, which will likely strengthen the incentive to make a confession more quickly than (before) others in order to receive a lighter sentence.

　Also, the terms of the Antimonopoly Act, which provide for a reduction in fines levied (leniency) for those reporting cartels and collusive bidding, take a first-come, first-served approach that is based on Social Dilemma theory. That is to say, it is an “encouragement to betray.” In short, the underlying concept is that cooperation among offenders will not be tolerated. There are still other examples of problems caused by “consistent cooperation.” There are players who always choose to cooperate in a Prisoner’s Dilemma. Even if betrayed, they do not betray in return. At first glance, these appear to be good-natured players. These are practicing turning the other cheek. However, would this really cause a player who chooses to betray, despite the other player cooperating, to repent? It is difficult to derive from this teaching the additional precept that it is wrong to betray. One of the academics researching the Prisoner’s Dilemma came up with the maxim that saints make normal people into sinners. In other words, he meant that those players who always cooperate make the other player betray them. Some academics also refer to players who only cooperate as “suckers” rather than “saints.” It means that a pattern of behavior characterized by consistent cooperation induces the other player to betray them. That is, it is better for player A to allow player B to realize that player A will also betray, and that cooperating with the other is desirable. (⇒ Reference “Does ‘tit for tat’ really lead to a better society?”)

Why do people skip the cleaning when it's their turn?

　After school is finished, it is time for those on the cleaning rota to get to work. The objective is for classmates working in turn to clean the classrooms. Although some people take the cleaning seriously, some skip it. Those who skip the work are “cheating,” so why do they do it? Which type are you?

　In fact, within the rota system, there is a flaw that makes people want to cheat and skip their turn. If all those whose turn it was did it properly, the classrooms would be cleaned quickly. However, when other people are cleaning, the impact of you skipping your turn has little effect. It may seem that for you to take the cleaning seriously when many other people are skipping their turn is kind of a wasted effort. In the end, you skip your turn because other people are skipping their turn, and the classroom remains uncleaned.

　So what can be done in order to prevent people from skipping their turn and to keep the classroom clean? One approach would be to tell the teacher that some were cheating (skipping their turn) and have them punished. However, if you were to do that, it might result in you being called a snitch. Try to think of what other approaches there might be. This problem is surprisingly difficult and, although more than half a century has passed since it was first pointed out, a variety of different solutions are still being proposed today. This problem is called the Prisoner’s Dilemma or the Social Dilemma. (⇒ Reference “What is the Prisoner’s Dilemma / Social Dilemma?”).

Will eels become extinct as a result of overfishing?

　In recent years there have been media reports of poor catches of eels. Nearly all the eels that we eat are farmed eels, but rather than being farmed for 100% of their life cycles (managed in the eel farm from egg production and fertilization i.e. artificial incubation), juveniles are caught at sea and brought up in eel farms. The life-cycle of the eel is still in the process of being deciphered, but it is thought that overfishing of juveniles is a major cause of poor catches. The only way to prevent overfishing is to control catch volumes, but even if one party exercises restraint, if other fishermen take the catch instead, it will ultimately lead to overfishing. Not only that, but those who hold back see lower incomes, while those who haul in large catches see higher incomes. Preventing fishermen from stealing a march on their competitors should be as easy as allocating catch quotas to each.

Why does doping not disappear?

　During the Summer Olympics of 2016 in Rio de Janeiro, there were sensational media reports of state-sanctioned doping by Russian athletes. There have also been sporadic problems with doping in sporting circles in Japan. It is known that the substances used for doping have a variety of side effects, but despite the damage to the health of the user, they do not cause problems for others. The problem associated with doping is, as may be imagined, that it constitutes behavior that goes against equitableness in sports and the spirit of fair play. But why does doping not disappear?

　If nobody were to dope, victories would be decided on the outcome of fair competition. If a competitor were the only one to cheat, they would be more likely to have an advantage over competitors, and more likely to win. However, if not one but multiple competitors were to dope, they would be back to square one, or worse, because trust in the results of competitions would have been harmed. Why are athletes unable to agree to self-restraint?