MAS models

Prisoner's Dilemma tournament model

What is the Prisoner's Dilemma tournament model?

　Although it is very important for people to cooperate with each other, sometimes it can be an extremely difficult problem. This is especially relevant in situations in which cooperation between different people results in beneficial outcomes for everybody, but in which the only person to benefit if that person decides not to cooperate is that same person.

　It is the prisoner's dilemma that expresses such difficult situations. Devised in the 1950s, this became one of the representative research themes of game theory. When facing this dilemma, how would you act to enable the two of you to cooperate?

　The Prisoner's Dilemma tournament model was devised to facilitate the examination of cooperative relationship building in such a dilemma. It is based on research announced by American political scientist Robert Axelrod in 1980. This is a fascinating model that uses unexpected methods to give us surprising pointers to building cooperative relationships.

Model rules

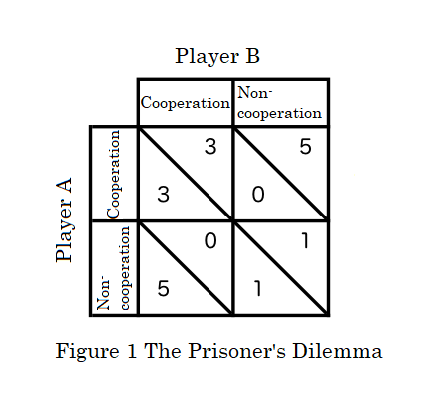
　First, a quick explanation of the Prisoner's Dilemma. (Please refer to Figure 1). The prisoner's dilemma expresses a situation that occurs between two people. You can choose between the options of cooperation and non-cooperation. The other person faces the same choice. Each makes their choice freely. The outcome is determined by the combination of your choice and the choice of the other person. Here, the result will determine the points scored by yourself and the other person.
For example, if you cooperate and the other person also cooperates, both sides receive three points. If you cooperate but the other person does not cooperate, you get zero points and the other person gets 5 points. If both sides choose not to cooperate, both sides get 1 point.

　How should one behave in order to obtain the maximum points in a Prisoner’s Dilemma situation such as that described above? We shall use the term “strategies” to describe rules relating to behavior. One can think of many possible strategies. For example, one could cooperate with the other person for as long as they cooperate with you, and refuse to cooperate again if the other person does not cooperate, and so on. Here we will gather together some of the strategies that have been devised to win the Prisoner's Dilemma tournament, use them in an actual match, and see what results.

　The strategies are referred to by their nicknames or the names of the people who devised them. For example, the strategy mentioned above was proposed by economist Milton Friedman, and has therefore been christened the Friedman strategy. The details of the respective strategies are explained below, and you are encouraged to refer to them. So, what happens in a tournament?

※This model does not reproduce the original exactly, but has been adapted while keeping in mind the spirit of the original.

Download Prisoner's Dilemma tournament model

artisoc or artisoc player (free) is required to execute the model.

Model highlights

　In the two tournaments sponsored by Axelrod, a tit-for-tat strategy won twice in succession. In this strategy the player first cooperates, then copies the other player indefinitely, selecting the option that the other player chose in the previous round. In other words, if the other player cooperates, then the first player cooperates, and if the other player does not cooperate, the first player chooses not to cooperate. It had been known previously that tit-for-tat was an effective strategy, and the researchers who participated in the tournament also knew this. Despite that, the tit-for-tat strategy emerged as the winner.

　Axelrod examined the strategies that performed well in the tournaments, and argued that they shared some characteristics. Strategies that performed well had the property of “niceness,” meaning that they did not betray others first. Another characteristic that he considered important in terms of getting a high score was that of “forgiveness,” meaning that betrayal would be excused. To put it another way, he argued that even in a situation in which stealing a march on the other player leads to high points, so that there is an incentive to betray them, demonstrating niceness and forgiveness led to cooperative relationships, and was linked to surprisingly high scores.

　Separately from the tournament, which was played in round-robin style among all strategies, people also tried modeling those strategies that performed well in a kind of evolutionary game, in which successful strategies that achieve good performance increase (or conversely, decrease for unsuccessful strategies) with each successive generation. The tit-for-tat strategy would also be expected to perform well in this struggle for survival. Exactly which strategy becomes dominant will vary depending on the combination of head-to-head matches, but it is certain that niceness is important.

　That the simple behavior of the well-known tit-for-tat strategy was effective in dealing with the dilemma, and that niceness and forgiveness were important even in situations where betrayal was effective, surprised many people and prompted a major debate. The points scored by a given strategy in the Prisoner's Dilemma vary depending on which strategy governs the other player, so the result is influenced by the strategies participating in the tournament. While the results produced by Axelrod were criticized as being in no way typical, and it was suggested that the outcome was dependent on the circumstances (issues that Axelrod himself recognized), on the other hand, the issue made clear by the tournament (that under certain conditions cooperative relationships could be built even in a dilemma situation) was also criticized as being no more than confirmation of what was already known from previous mathematical research.

Strategies participating in the tournament

・Tit-for-tat strategy (TFT); niceness/forgiveness
Chooses cooperation on the first move, then cooperation if the other player selects cooperation, or non-cooperation if the other player selects non-cooperation.
・Forgiving strategy (tit-for-two-tats, or TTT); niceness/forgiveness
Chooses cooperation on the first move, but if the other player selects non-cooperation twice in succession, selects non-cooperation on the next move.
・Reverse tit-for-tat (RTF); nastiness/forgiveness
Chooses non-cooperation on the first move, then cooperation for the next move if the other player selects cooperation, or non-cooperation if the other player selects non-cooperation.
・Nydegger strategy (NYD); niceness/forgiveness
　　Uses a tit-for-tat strategy for the first three movies. After that, the NYD determines whether to cooperate or not depending on the pattern of the combination of its own and the other player’s choices over the preceding three moves. Various rules are put in place, such as if both the NYD and the other player chose non-cooperation for each of the preceding three moves, the NYD selects cooperation, or if the other player also chooses cooperation (except in cases where the NYD chose non-cooperation three moves earlier), then the NYD selects non-cooperation. As the strategy was created to be used in experiments with people, it is basically cooperative but is designed not to be stupid.
・Grofman strategy (GRO); niceness/forgiveness
　　Basically selects cooperation. When the other player and the GRO strategy make different choices, the GRO will select cooperation for the next move with a probability of 2 out of 7 times. It has a tendency to choose non-cooperation when the other player tries to steal a march, or when stealing a march over the other player, but when mutual cooperation has been established with the other player, it will continue to cooperate, and it will also choose cooperation even when faced with non-cooperation.
・Shubik strategy (SHU); niceness/forgiveness
　　Basically chooses cooperation, but if the other player chooses non-cooperation, will select non-cooperation on its next move. The number of times it selects non-cooperation is initially set to just 1, but if mutual cooperation collapses, it will increase the number of times it chooses non-cooperation by one move each time.
・Stein strategy* (STN); niceness/forgiveness
　Cooperates for the first four moves, then uses a tit-for-tat strategy.
・Friedman strategy (FDM); niceness/non-forgiveness
　　Selects cooperation on the first move, but if the other player chooses non-cooperation even once, switches to non-cooperation until the end of the game.
・Davis strategy (DVS); niceness/non-forgiveness
　　Selects cooperation for the first 10 moves. If the other player chooses non-cooperation even once during that time, subsequently switches to non-cooperation. Otherwise it cooperates.
・Graaskamp* strategy (GRS); nastiness/non-forgiveness
　　Uses a tit-for-tat strategy for the first 50 moves. Thereafter, chooses non-cooperation every 5 to 15 moves. The number of moves between moves in which non-cooperation is selected is determined at random.
・Downing strategy* (DOW); nastiness/forgiveness
　　This strategy is based on the hypothesis that the other player’s choice is determined probabilistically based on the DOW’s most recent choice, and maintains the estimated probability of the other player choosing cooperation if DOW chooses cooperation on its next move, and the estimated probability of the other player choosing cooperation if DOW chooses non-cooperation on its next move. The initial value for the two probabilities is 50%, but this is updated as the game progresses. The strategy selects options that are estimated to be effective over the long term.
・Downing-Revised strategy * (DWR); niceness/forgiveness
　　This is the same as the Downing strategy, but the initial values of the two probabilities are different. The estimated probability of the other player choosing to cooperate on their next move after DWR has chosen cooperation is set at 100%, and the estimated probability of the other player choosing to cooperate on their next move after DWR has chosen non-cooperation is set to 0%.
・Feld strategy (FLD); nastiness/forgiveness
　　Uses a tit-for-tat strategy at first. When the other player chooses cooperation, FLD gradually reduces the probability of cooperation being selected. By the end of the game it seeks to reduce this to 50%. When the other player chooses non-cooperation, FLD chooses non-cooperation on its next move, without exception.
・Joss strategy (JOS); nastiness/forgiveness
　　Chooses cooperation on its first move, and if the other player chooses cooperation, JOS has a 90% probability of choosing cooperation on its next move (a 10% probability of non-cooperation). If the other player chooses non-cooperation, JOS chooses non-cooperation on its next move, without exception.
・Tullock strategy (TLK); nastiness/forgiveness
　　Cooperates for the first 10 moves. Subsequently selects cooperation with a probability 10% lower than the frequency with which the other player chose cooperation during that period.
・Random strategy (RDM); nastiness/non-forgiveness
Determines whether to cooperate or not to cooperate randomly on every move.
・All-D strategy (ALD); nastiness/non-forgiveness
　　Always chooses non-cooperation.
・All-C strategy (ALC); niceness/forgiveness
　　Always chooses cooperation.

※The strategy rules for this model do not reproduce the original paper exactly, but have been adapted while keeping in mind the spirit of the original. Rules that attempt to get points at the end of the game by betraying the other player, and rules that attempt to infer the strategy of the other player and react to it, have been omitted.

※※In the explanations for the rules, “niceness” means no possibility of betraying others first; “nastiness” means the possibility of betraying others first; “forgiveness” means there is a mechanism for restoring mutual cooperation after the other player has used betrayal; “non-forgiveness” means there is no mechanism for restoring mutual cooperation after the other player has used betrayal

This website uses cookies.

MAS models