MASのモデル
自然渋滞発生モデル
自然渋滞発生モデルとは
高速道路などで発生する自然渋滞を、マルチエージェント・シミュレーションのモデルとして再現したモデルです。
(⇒<自然渋滞の発生>を参照)
半径37mの円状のテストコースを空間として定義し、自動車エージェントをテストコース上に等間隔に22台配置します。 各自動車エージェントは、以下のルールにもとづいて行動します。
・速度30km/hで走行する
・前方車両と近づきすぎたらブレーキを踏む
・前方車両と十分な車間距離がある場合には30km/hまで加速する
・シミュレーションステップごとにわずかな速度のゆらぎとして±0.02km/hを与える
モデルの見どころ:車両密度と交通容量
自然渋滞は、車両密度の高い、車間距離が詰まった状況で起きやすくなります。 自然渋滞発生モデルを用いて、車両密度と交通流量の関係を検討することができます。
テストコース上に車両の通過台数を計測するポイントを設置します。 そして、テストコース上に配置する車両台数を1台から徐々に1台ずつ増やしたシミュレーションを実施し、それぞれ10分間分を100試行行います。 シミュレーション結果をグラフに示します。 横軸がテストコース上の車両台数(車両密度)で、縦軸が10分間あたりの計測ポイントの通過台数(交通流量)を示します。
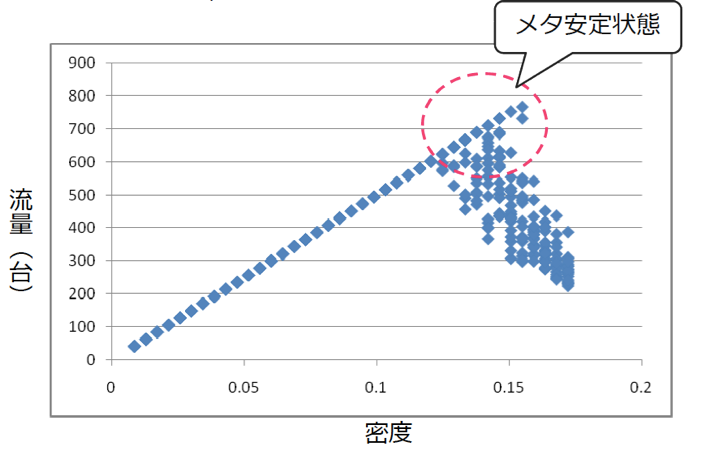
車両密度が低い場合の流量は、台数が増えるに伴い流量が単調増加傾向にありますが、ある程度密度が高くなると極端に流量が低くなってしまうケースが現れ始めます。 このようなケースが渋滞の発生した状況です。 車両密度が低い場合は、渋滞は起こらず、車はスムーズに流れますが、車両の数自体が少ないので交通流量は少なくなります。 車両密度が高くなるにつれて、車両の台数が増えるので、交通流量も増えていきます。 しかし、車両密度が高くなったことで渋滞が発生すると、車両がスムーズに流れなくなり、交通流量は逆に減っていきます。 車両密度を上げていけば、やがては車が全く動けなくなることになります。
注目すべきなのは、車両密度が約0.12から0.15の間では、同じ密度でも試行によって非常に交通流量の高い状態と低い状態の両方が存在し、結果にばらつきがあることが分かります。 この密度では、車がスムーズに流れるときと、渋滞が起こってしまって交通流量が激減してしまうときの両方が起こりうることを示しています。 この密度で車がスムーズに流れることは可能ではあるのですが、たいへん不安定な状態でもあり、何らかの拍子に誰かがブレーキを踏むなどのイベントが発生した途端に流量の低い状態に陥ってしまうのです。 このような不安定な安定状態のことは「メタ安定状態(準安定状態)」と呼びます。 自然渋滞が発生するときには、道路上の車列がその直前に「メタ安定状態」になっていると考えられています。
このような渋滞の発生メカニズムを、非常にシンプルに描き出したのがASEPモデルです。 詳しくは参考文献に挙げた西成先生の書籍を参考にしていただきたいのですが、シンプルなモデルを用いることで、このような現象がなぜ起こるのかを明らかにすることができます。 車両の動きに惰性があり、一度止まった車がすぐに元の速さに戻るわけではないことが、このメタ安定状態を生み出しています。
メタ安定状態(準安定状態)
車の台数が増加し、車両密度が非常に高くなっているのに車がスムーズに流れるというメタ安定状態は、何らかの拍子に突然に渋滞という真の安定状態となってしまう「不安定な」安定状態です。 長い時間を経たり、さまざまなゆらぎを与えたりすれば、最終的には「真の」安定状態へと移行するうたかた(泡沫)の状態ということになります。
非平衡系において、要素間の相互作用のなかで、初期状態と経路依存のからみで、真の安定状態にいたる中途に出現する一時的な安定状態というのが、メタ安定状態(準安定状態)です。 渋滞を起こしかけている車両だけでなく、過冷却状態にある水(工夫すれば、水を氷にすることなく、−40℃くらいまで冷やせるそうです。衝撃を与えれば氷になります。)や ガラス(高温に加熱して液体になったケイ酸を比較的急速に冷やしたときに生まれます)は、メタ安定状態にあると考えられています。
ガラスの例からも分かるように、「一時的」で「不安定」とは言っても、それは真の安定状態と比べるからであって、私たちの目からは十分に安定的に見えるメタ安定状態はたくさんあります。 ぜひ探してみましょう。
参考文献
[1]. 西成活裕「渋滞学」, 新潮社, 2006
[2]. 西成活裕「図解雑学 よくわかる渋滞学」, ナツメ社, 2009
[3]. JAF「社会実験 ~渋滞吸収理論を実践する~」, https://www.youtube.com/watch?v=TP_7uUG4e3o (2023/12/16確認)
|
自然渋滞発生モデル 基本情報 【モデルタイトル】:自然渋滞発生モデル artisoc Cloud artisoc4【モデル考案者】:構造計画研究所 森俊勝 【artisocサンプルモデル作成者】:構造計画研究所 森俊勝 【artisocサンプルモデル作成日】:2008年6月1日 ASEPモデル 基本情報 【モデルタイトル】:ASEP(Asymmetric Simple Exclusion Process)モデル artisoc Cloud artisoc4【モデル考案者】:Frank Spitzer 【モデル発表年】:1970年 【artisocサンプルモデル作成者】:光辻克馬 【artisocサンプルモデル作成年】:2017年 |
