MASのモデル
満員電車モデル
モデルの概要
電車の車内混雑のモデルを作成しました。
一般的には車内混雑の指標として『乗車率』という値が使われますが、『乗車率』だけでは感覚的にどれくらい混雑しているかを把握しづらいのではないでしょうか。
このモデルは車内混雑を可視化するとともに、ルールに基づいて現実に近い状況を表現するというモデリング方法の一例として作成しました。
車内混雑をモデル化するために、次の2つのルールで表現しました。
- 他人と近すぎないように距離を置く
- 距離が近い他人と視線が合わないように体の向きを変える
この2つのルールによって、車内の混雑を以下のように再現できます。
80%乗車率の状況
乗客のうち、黒色で表示されている人は快適な状態、紫色は他人との距離が近いため不快な状態、
オレンジ色は他人と体が触れ合う状態、赤色は身動きできない状態を表す。
モデルの詳細
乗客同士の斥力
Pushkarevら[1]の研究では、立っている人たちが感じる混雑は以下の表のような形で整理されています。本モデルでは乗客一人ひとりが周囲に立っている他人との距離(重心間の距離)によって感じる混雑状態とそれに基づいた斥力による行動を用いています。
|
状態 |
体感 |
他人との距離 (重心間) |
1人当たりの |
斥力による行動 |
|
Jammed |
身動きできない |
0.5m未満 |
0.2m²未満 |
2歩離れる |
|
Congested |
体と体が触れ合う |
0.5~0.6m |
0.2~0.3m² |
1歩離れる |
|
Constrained |
他人との近さによる不快感 |
0.6~0.9m |
0.3~0.7m² |
0.5歩離れる |
|
Comfortable |
快適 |
0.9m以上 |
0.7m²以上 |
斥力なし |
周囲のすべての人による斥力をベクトル加算し、最終的に求まったベクトルの方向に移動速度に基づいた距離分を移動します。
移動速度
Pushkarevら[1]は混雑している中を歩ける速度が一人当たりのスペースによって変わると述べており、それを基準に本モデルでも以下の式を用いて計算します。
向きの調整
他人の視線を意識する場合のパーソナルスペースについて、Pushkarevら[1]は1.2mという値を用いています。本モデルでも各エージェントが1.2m以内に他人が立っている場合に、視線が合わないように体の向きを変えるようにしています。
シミュレーションの詳細
乗車率の定義
乗車率は以下のように計算されます。
乗車率の定員の決め方は、JIS E 7103:2006 で以下のような規格が定められています。
「立席定員は,腰掛用の床面積及び腰掛前縁から250mmの床面積を除いた客室床面積のうち、(中略)乗客1人当たりの占める広さは0.3m2とする。」
上記の計算から、例えばJR山手線の中間車両の定員は160人となります[2]。そのうち、51人が座席に座ることができます。JR山手線の中間車両を参考にし、車内の混雑状況を再現してみました。
車両における座席の配置の例
シミュレーション・ステップについて
1ステップは、秒換算すると0.5秒程度を想定しています。
停車と乗降車
シミュレーション中、65ステップ目で駅に到着し、それから35ステップをかけて降車します。そのあと、電車に乗る人が1ステップで乗車して車内を移動します。この乗降車のパターンが100ステップごとに繰り返します。
乗り降りすることで一時的に混雑レベルが変わりますが、乗客が自分のスペースを確保するために車内を移動することで徐々に安定していきます。
混雑レベルの指標
乗車率は車両全体の観点からの混雑度合の指標ですが、一人ひとりが感じる混雑度合の指標として、以下の三つを出力しています。
1. Comfortable, Constrained, Congested, Jammed状態の割合
2. 他人との最短距離の平均 [m]
3. 1人当たりのスペースの平均 [m2]
125%乗車率の場合の混雑レベルの3つの指標
上記のように混雑レベルを直接的に表す指標の他、混雑レベルの影響を間接的に受ける「平均降車時間」という指標も用いています。
リュックを背負うことの影響について
本モデルの拡張の一例として、リュックを背負うことの影響について検討してみました。
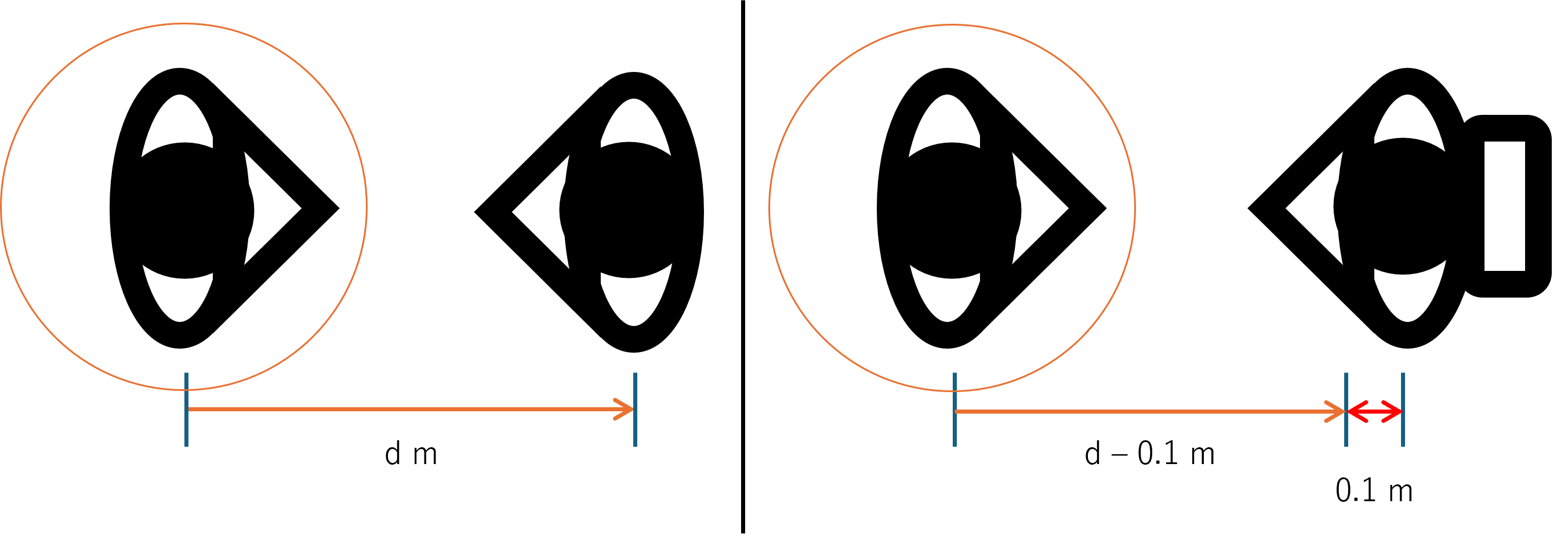
隣の人がリュックを背負わない場合(左)とリュックを背負う場合(右)の距離計算。
(リュックの形状に関わらず、他人がリュックを背負う場合に重心間の距離から0.1mを引く。)
乗車率80%で、リュックを背負う人の割合が50%の車内の様子
リュックを背負う人が占めるスペースは、リュックを背負わない人より大きくなります。そのため、リュックを背負う人の割合が増えると、一人当たりのスペースが狭くなり、同じ乗車率でも混雑レベルが悪化します。
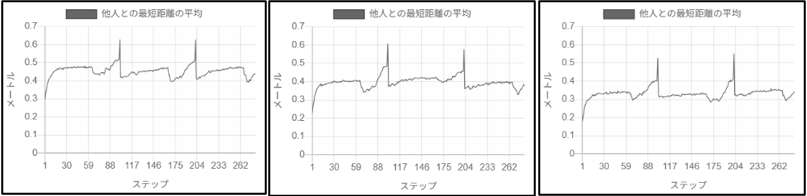
具体的には、以下のグラフは同じ乗車率の状態で、リュックを背負う人の割合を変えた場合の他人との最短距離を示しています。リュックを背負う人の割合が0%の場合は0.47m程度だった距離が、50%の場合は0.4m、100%の場合は0.34mまでと著しく減っていることがわかります。
125%乗車率でリュックを背負う人の割合が0%(左)、50%(中央)、100%(右)の場合の他人との最短距離の比較
(一時的に他人との距離が長くなるのは、降車により車内の人数が一時的に減るためです。乗車によって再び人数が増えると距離が元のレベルに戻ります。)
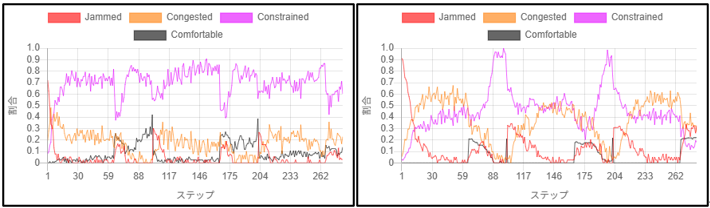
以下の混雑レベルのグラフでもリュックを背負う人の割合を増やすことで、混雑レベルが悪化しているように感じる人(赤:Jammed、オレンジ:Congested)の割合が増えることがわかります。
80%乗車率でリュックを背負う人の割合が0%(左)と100%(右)の混雑レベルの比較
次のステップ(やってみよう)
上記のモデルを応用して、リュックを前に抱えた場合はどうなるか、大きいスーツケースを持っている乗客が多い場合はどうなるかなどを検討することができます。
また、乗り降りをスムーズにするための施策を検討することができます。
- 乗り降りが最も快適な場所、混雑の影響が最も小さい場所または最も大きい場所の分析
- 他の乗客が降りやすくするために通路を空ける、一旦降りて再度乗車する等の支援行動
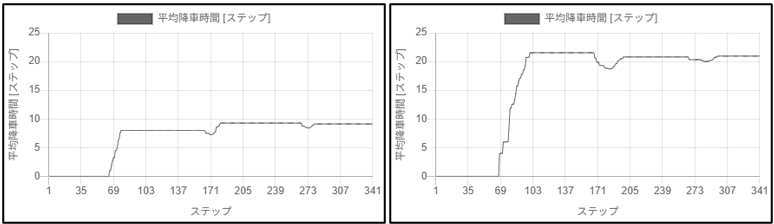
- 混雑レベルによる平均降車時間の比較(下図)
平均降車時間の推移の比較:左:乗車率80%、右:乗車率125%
参考文献
[1] Pushkarev & Zupan 1975: Urban Space for Pedestrians: A Report of the Regional Plan Association, MIT Press, 79. https://rpa.org/work/reports/urban-space-for-pedestrians
[2] 松島千裕,他:「JR東日本 E235 系量産車 一般形直流電車」総合車両製作所技報, Vol.6, 94-99,(2017),(株)総合車両製作所
|
満員電車モデル 基本情報 【モデルタイトル】:満員電車モデル artisoc Cloud【モデル考案者】:シロトリヤトゥシャール 【モデル発表年】:2025年 |