身の回りの複雑系
人のつながり
社会は人と人とのつながりでできている
自分の周りには大勢の人が存在し、人と人とがつながることで社会をつくっています。 今、通っている学校も、毎日練習している部活も、住んでいる街も一種の社会であり、誰もがいろんな社会に属しながら生活をしています。
さらにスマートフォンやパソコンなどにより、遠くにいる誰かと話をしたり、SNSでチャットしたり、インターネットで情報を仕入れたりと、 身の回りとは違った社会にもつながることができます。

私たちは様々な社会とつながることで、自分の知らない情報を得たり、体験したりします。 一方で、つながりが強くなり過ぎることで返事が面倒など逆に重荷になったり、寝不足になったりするのではないでしょうか。 アドラー心理学では「すべての悩みは対人関係の悩み」と言っています。 ちょうどいい感じで社会とつながりを持ち、人間関係を保つためには、どうすればよいでしょうか?
見えない人間同士のつながりを見てみよう
人間同士のつながりを目で直接見ることはできません。もし見えるとするとどのような形になっているでしょうか。
それを知るために、ここで1つ実験をしてみましょう。 クラス全員にアンケートし、最近1週間で話しをしたクラスメートの名前を紙に書いてもらいます。 次にノートの上にクラス全員分の名前を書き、話しをした人同士を線で結びます。 すると、網目状の模様が出てきます。 この網目をよく見ると、たくさんの人とつながりを持つ人がいる一方、つながりが少ない人がいることが分かります。
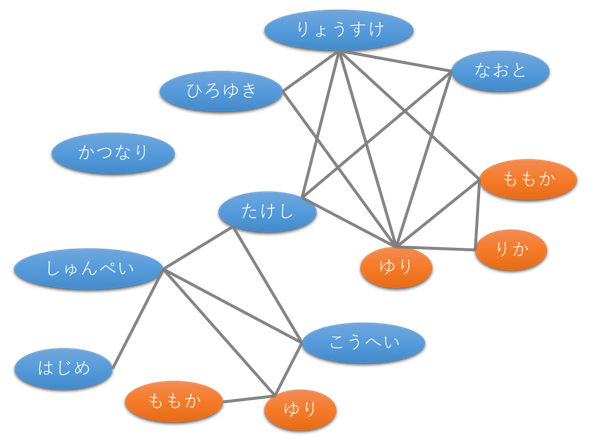
次に、自分と誰かが何人の人を介してつながっているかを調べてみましょう。 仲の良い人は直接つながり、それほど付き合いのない人はつながるまでに何人か必要になってきます。
自分から一番遠い人を探して、話しかけてみると、自分の知らない新しい発見があるかもしれません。
世界の誰とでも平均6人でつながっている!?
クラスのつながりが分かったところで、次は世界に目を向けてみましょう。 国連の報告によると、2016年現在で地球上に約73億人の人が住んでいます。 世界の中の誰か(例えば海外の有名人)と何人くらいの人を介してつながっているのでしょうか。1千人?1万人?100万人?
これを社会実験で確かめたのが、スタンレー・ミルグラムです。 ミルグラムは、新聞広告で「差出人」を募集し、見ず知らずの誰かを「最終受取人」とした手紙に 差出人の名前、職業、住所を記載し、自分の知り合いで「最終受取人」を知っていそうな人に手紙を送るように依頼しました。 これを知り合い同士のつながりを通して、最終受取人にたどり着くまで繰り返しました。
無事に最終受取人に手紙が届いたケースについて、経由した人数を調べてみたところ平均 5.5 人でした。非常に少ないですね。 これは『六次の隔たり』(「次」とはつながりの数のこと)として有名になり、世の中は意外と狭いかもしれないという「スモールワールド」の考え方が広まりました。
「スモールワールド」を理解するために「ケビン・ベーコン・ゲーム(The Oracle of BACON)」を紹介します。 ケビン・ベーコンは米国の有名俳優で、いろんな映画に出演しています。映画の共演者をつながりとして、ある俳優が何人の俳優を介してケビン・ベーコンとつながるかを測ることができます。 ※ローマ字で入力すると日本人俳優のつながりも調べることができるので、試してみましょう。
スモールワールドネットワーク
世界中の誰とでも平均6人の知り合いでつながっている「スモールワールド」とはどのようなつながりでしょうか?(⇒<世界の誰とでも6人以内でつながっている>を参照)
「スモールワールド」を数学を使って研究したのが、ワッツとストロガッツです。 (⇒<ワッツ・ストロガッツモデル>を参照) では、実験してみましょう。
① クラスのみんなで輪になって、隣どうし手をつなぎます。
② 誰か一人を決めて、自分から何人の人を介してつながっているかを数えます。
③ これを全員分について数をかぞえ、平均を求めます。
④ 次に、誰か二人をランダムに選び、ヒモでつなぎます。
⑤ また、全員分について何人の人を介してつながっているかを数え、平均を求めます。
ヒモを何本か用意して実験してみると、ヒモの本数を増やしていくと、平均の数が驚くほど小さくなっていくことを発見しました。 この特徴を「スモールワールドネットワーク」と呼びます。
親友はいざというときに頼りにならない?
個人的な悩みや相談ごとがあった場合、世界中の人がつながっていたとしても、信頼のおける友人や家族?に相談するのではないでしょうか。 そこで、人間関係の深さ(強弱)について考えてみましょう。
ここで質問です。「人生」において誰が一番頼りになるでしょうか? 日常的には親友や両親が頼りになりそうですが、「人生」となると、どの学校に進学するか、どの会社に就職するか、誰と結婚するか、いつ子どもをつくるかなど、親に頼れないことも多々あります。
マーク・グラノヴェッターは、人生の大きなイベントの1つである「就職」について研究しました。 彼の書いた論文( 「弱い紐帯(ちゅうたい)の強さ」※「紐帯」とはつながりのこと )では、就職先を見つけるときは、 (やや直感とは異なりますが)強い友人関係よりも、弱い社会的絆の方が重要であることを示しました。 つまり親友や両親よりも、年に数度会う親戚のおじさん、おばさんの方が頼りになるかもしれないということです。
その理由は、緊密な友人関係の中では知りうる情報も似たようなものになりがちであり、弱い紐帯が外の世界との架け橋となることで、新しい情報を得ることができるからです。
仲が良いもの同士で集まるのもよいですが、たまには違ったメンバーと話しをしたり、外の世界に触れることもおすすめします。
口コミとパニック
口コミによって、映画が大ヒットしたり、動画コンテンツが急速に世界中で話題になったり様々な流行がつくられます。 一方で悪い噂などの情報もインターネットの普及で簡単に急速に広まり、ブログの炎上など社会問題になっています。
人のつながりが招いた社会現象として、豊川信用金庫事件を紹介します。 事の発端は、豊川信用金庫に就職が決まった女子高校生に友人が「信用金庫は危ないよ」とからかったことにはじまります。 友人は、信用金庫は強盗が入ることがあるので危険という意味で話したのですが、何人か人を介することでいつのまにか 「豊川信用金庫が倒産する」と噂(デマ)が伝えられました。 結局、20億円の預貯金が引き出される事件になりました。
何気ないネット上の会話やつぶやきが誤解され、拡散されるかもしれません。 まさに、口は災いの元ですね。
身の回りはネットワークだらけ
夏、蚊などの虫が家の中に入ってこないように「網戸」を使います。 霧が立ちこめる朝、公園に散歩に行くと、露を宿した「クモの巣」を簡単に見つけることができます。 どちらも規則正しい「ネットワーク」です。
学級では「連絡網」があらかじめ決められていることが多いと思います。 自分Aの友達Bの友達Cは、やはり自分の友達だという場合も、ABCが互いに結びついている「友達の輪」になっています。 こうした人間同士の結びつきも「ネットワーク」と言えます。 顔見知りの人の数はだれでもそんなに多くないのに、知り合いから知り合いへとたどると、かんたんに世界中の人に行き着くのだそうです。 (⇒<世界の誰とでも平均6人でつながっている!>を参照)
東京のような大都会では地下鉄路線が「網」のようにつながっており、複雑すぎて乗り換えに迷うことも多いですが、慣れてくるととても便利です。 JRの路線も、北海道から本州を経て、四国や九州までつながっています。 飛行機の航路の「網」は、新千歳・羽田・大阪・福岡・那覇といった「ハブ」空港を結ぶ幹線「網」と「ハブ」空港と地方空港を結ぶローカル線が目につきます。
発電所から変電所そして各家庭へ電気が流れているのも電線「網」(パワーグリッド)のおかげです。 都市ガスや上水道、下水道もライフラインと呼ばれることがありますが、こうした「ライン」は「ネットワーク」になっています。 地上波のテレビ番組も、キー局を中心とする「ネットワーク」になっています。携帯電話の中継局どうしも「ネットワーク」になっています。 (⇒<バラバシ・アルバートモデル>を参照)
このように、私たちの周りを見渡すと、多種多様なネットワークだらけなのです。 一見ネットワークのように見えなくても、そのように呼べる特徴を持っている「つながり」が無数にあります。 (⇒<ネットワークはどのようにつながっているの?>を参照)
週末の家族ドライブで渋滞に出会ったしまったとき、抜け道を迂回できるのは、道路「網」だからです。 鉄道の不通や運転見合わせの際の「振り替え輸送」が可能なのも、鉄道各社の路線が「網」のようにつながっているからです。
ところが、一カ所で送電線が切断されると、そのショックが送電網を伝って広がり、広範囲で停電が起こることがあります。 一カ所の信号機の不具合で、いくつもの路線が何時間も運転見合わせになることもあります。 つながっていると便利なだけではなさそうですね。
ネットワークはどのようにつながっているの?
「ネット」状になっているもの・「ネット」状に作られているものならなんでもネットワークです。 それゆえに、身の回りには、さまざまなネットワークを見て取ることができるのです。
しかし、規則正しい格子状になっている網戸と数少ない空港から放射線状に航空路が延びている航空路線網とでは様子がかなりちがいます。 それでは高速道路網はどちらに近いでしょうか。
ABCの三人は互いに友達同士の場合もあるでしょう。 しかし、BさんもCさんもAさんのことを好きだけど(好きだから?)、BさんとCさんは仲が悪い場合もあるでしょう(三角関係)。 もっと一般的に、三人の間にはどのような関係が成立し得るでしょうか。 人数が増えるとどうなるでしょうか。
鉄道路線網を利用する場合もいろいろと考えられます。 A駅からB駅に行くのに、最短時間経路、最小乗り換え経路、最低料金経路などがあるはずです。
逆に、望ましいネットワークの設計・構築という考え方もあるでしょう。 たとえば、学級の全員になるべく少ないクラスメートを経由して連絡したい。 どこか1カ所が不通になっても迂回路がある道路網を作りたいが、建設費を抑えたい。
ようするに、ネットワークの捉え方にはいろいろあります。 なんとなく特徴の違いは分かるのですが、もう少し客観的に違いを捉えた方が議論の土台ができるでしょう。 ある特定のネットワークの全体的特徴を表すには、どのような指標を用いると的確になるでしょうか。
近年、ネットワークへの関心が深まり、さまざまな考えが提唱されています。 ネットワークの大局的な特徴を捉えて、特別な名前をつけたり、さまざまは指標が導入されたりしています。 (⇒<つながりを分析する>を参照)
つながりを分析する
人間関係以外にも、身の周りには交通網、脳細胞のつながり、WEBのリンク関係など様々なネットワークが存在します。 ネットワーク分析とは、実体(ノード)そのものではなく、実体間のつながり(リンク)に着目した分析手法です。 ネットワーク分析により、種類や分野の違うネットワーク同士を比較したり、ネットワークの特徴や状態の変化を説明することができます。
・【次数分布】
次数とはつながりの数のことで、皆が同じくらいの数のつながりを持つか、数人の人が極端につながりが多いのかのばらつき度合いを見ることです。 東京の羽田空港や大阪の伊丹空港は多くの空港とつながっていますが、北海道の利尻空港、沖縄の宮古空港は1箇所としかつながっておらず、ばらつきが大きいです。 一方、高速道路ではある地点に接続される道路の数に大きな差はありません。これは物理的な制約によるのも一因ですが、1箇所にクルマが集中して渋滞を発生させないための工夫とも言えます。
・【平均最短距離(平均距離)】
2つのノードを最短のリンク数で結んだときの平均値のことです。 世界の誰かと誰かが6人の知人を介して結ばれるということは、人間関係は平均最短距離がとても短いネットワークだと言えます。
・【クラスター係数】
自分の知り合い同士が知り合い(三角関係)である割合のことです。 同じクラスのメンバーは、お互いの顔と名前が一致するのでこの値が高くなりますが、学校や学年が違うと知り合いが少なくなるのでこの値は低くなります。
・【中心性】
誰がネットワークの中心かを表す値のことです。 例えばクラスの中心は誰でしょうか?学級委員長はクラスを代表していそうですが、クラスの中の一番の人気者もいます。担任の先生がクラスをまとめていますが、クラスの中心というとやや違う印象があります。 中心と言ってもいろいろな定義があり、次数中心性はより多くのリンクがつながっている頂点、媒介中心性は平均距離を求めるときに通る数が多いノード(誰かをつなげる力が大きい)を選びます。
・【コミュニティ構造】
リンクが密なところをコミュニティと言います。 クラス、部活、塾、地域のコミュニティ、さらにはSNSの中のコミュニティなど、ひとりの人がいろんなコミュニティに属しており、人間関係はコミュニティ構造を持つと言えます。 では、コミュニティ構造はどうやって形成されるのでしょうか? 人種による住み分けをテーマに研究した「シェリングの分居モデル」や話す言葉や文化の変化をテーマに研究した「アクセルロッドの文化変容(文化の流布)モデル」はそのヒントをおしえてくれるかもしれません。
ネットワーク分析では、主に3つの性質でネットワーク同士を比較します。
・スケールフリー性
一部のノードが膨大なリンクを持つ一方、ほとんどのノードが少ないリンクを持つという性質です。 スケールフリー性の実例として、映画の興行収入を見てみましょう。 2016年の映画の興行収入は総額で2,355億円でした。 1位の青春アニメが大ヒットして235億円、2位は宇宙戦争モノの続編で116億円でした。 年間1,000本程度の作品が上映されるので、2億円程度の興行収入があれば平均的ですが、1位はその100倍もの成績を収めました。 さらに上位10タイトルを合計すると838億円で、映画の興行収入の1/3はたった1%の映画からもたらされていることが分かります。 スケールフリー性は映画に限らず、ベストセラー本やネット上の検索数など、みんなの興味や関心が時間とともに変化し、集中するネットワークで見られる特徴です。 (⇒<バラバシ・アルバートモデル>を参照)
・スモールワールド性
任意の2つのノードが、中間にわずかな数のノードを介するだけで接続するという性質です。 世間って狭いなって思うことが、たまにあるのではないでしょうか? 「ケビン・ベーコン・ゲーム(The Oracle of BACON)」 (たいていの俳優や女優は、出演した映画の共演者をたどっていくとケビン・ベーコンに行き着けるというゲーム)で人間関係のスモールワールド性を体感してみましょう。
任意のノードがリンクする2つのノード同士がリンクするという性質です。知人同士が知り合い(三角関係ですね)であることを意味します。 SNSを使って昔の同級生を探したり、グループに登録して新しい友達ができたり、出会いの機会が増えると社会全体のクラスター性は段々と高まっていくのかもしれません(但し、お互い同士を忘れなければの話しですが)。 ネットワーク分析の研究は、「ワッツ・ストロガッツモデル」と「バラバシ・アルバートモデル」が発表されたことをきっかけに、新しいパラダイムとして大いに注目され、数多くの新しい発見が生まれました。 20世紀の科学は、現象を要素に分解して理解するアプローチ(「還元主義」と呼びます)で発展してきました。21世紀の科学は、ネットワークを前提として要素同士の関係性を理解するアプローチ(「ネットワーク思考」と呼びます)を使うことで、新しい発見があるかもしれません。




