MASのモデル
流行伝播モデル
どんなモデル?
ペスト、天然痘、スペイン風邪といった感染症の大流行は多くの犠牲者を出しました。 近い将来においても、新型インフルエンザなどの感染症の流行は、人類全体にとっての大きな脅威です。 感染症の流行については、疫学の分野において20 世紀初頭より数理的なモデルによる分析の試みが行われてきました。 この努力は今も続いており、様々に工夫をこらした研究が行われています。その出発点となっているのが、 ケルマックとマッケンドリックの第一論文 (Kermack and McKendrick 1927)で発表されたSIR モデル(なぜこんな名前なのかはあとで説明します)です。 流行伝播モデルは、このSIR モデルの基本的仕組みを、エージェントベースのシミュレーションにしたものです。
もともとのSIR モデルは、ミクロな感染プロセスについて仮定をおいて、マクロな感染プロセスについての常微分方程式系を構築したものでした。 ここで紹介する伝播モデルでは、住民間の感染プロセスそのものをエージェントベースのシミュレーションモデルにしました。
SIR モデルは、感染症の流行についてのモデルですが、その発想は、病気だけでなく噂の伝播や新製品の流行など、 さまざまなものの伝播や流行の社会現象についてのモデルとしても用いることができます。
モデルのルール
流行伝播モデルは、感染症にかかる可能性のある人々で構成されているひとつの共同体を表しています。 この共同体の人々は、以下の3つ(場合によってはもう少したくさん)の状態のうちのどれかにあります。
(1)感受性者(Susceptible) =まだ病気に感染していなくて感染の可能性のある状態の人 (2)感染者(Infectious) =病気に感染して、感染させる能力のある状態の人 (3)除去者(Removed) =病気から回復して免疫保持した状態、あるいは物理的制度的に隔離されて感染させる能力を封じられた状態、あるいは病気により死亡した状態の人 ※潜伏感染者タイプ1(Exposed) =感染しており感染させる能力はまだ持っていない状態の人 ※潜伏感染者タイプ2(Exposed) =感染しており感染させる能力を持っているが、それがまだ誰にも分からない状態の人
感受性者のことを「S」、感染者のことを「I」、除去者のことを「R」、潜伏感染者を「E」と表します。 人々の多くは、最初「S」の状態から始まります。感受性者は感染者と接触することにより感染し感染者「I」となります。 時間がたつと感染から回復し免疫を保持することにより除去者「R」となります。 (場合によって、「隔離された」あるいは「病気により死亡した」と考えることができます。 つまり感染症の流行のことだけを考えるなら、病気から回復して免疫を得た人も、病気で死んだ人も同じということです。怖いですね。) こうして、人々が「S」「I」「R」の状態のあいだを移行するので「SIRモデル」といいます。
S→I→Rのパターンが基本となります。S→I→Rのパターンは、麻疹、水痘、風疹のように、感染した者がその後長期にわたって免疫を獲得する主に小児性の感染症や、 致死性が高く感染者を病死させることで除去者に移行させる感染症の分析に適しています。 感染症の性質により、SIR以外にも、いくつかの異なるパターンを考えることができます。
SISパターン:
感受性者は感染者と接触することにより感染し、時間がたつと感染から復帰します。 免疫の効果を無視することができて、感染から復帰した人が感染前と同じように感染の可能性にさらされているような場合は、このSIS パターンで表すことになります。 一般的な風邪や、淋病などの性感染症のように再び感受性者にもどる感染症の分析に適しています。
SIパターン:
感受性者は感染者と接触することで感染しますが、時間がたっても感染から復帰することはありません。 もっともシンプルなパターンです。このような場合は、このSI パターンで表すことになります。 比較的症状の軽い呼吸器系統の疾患に適しています。
SEIRパターン:
感受性者は感染者と接触することにより感染します。 人々は感染してもすぐに発症せず、感染しているけれども感染力のない潜伏感染者(E)になります。 (あるいは感染力のある潜伏感染者とすることもできます)時間がたつと感染者となり、さらに時間がたつと感染から復帰し免疫を保持する除去者となります。 はしかや耳鼻腺炎あるいはエイズなど潜伏期間の考慮が必要なものはこのパターンが適しています。
SIRSパターン:
感受性者は感染者と接触することにより感染し、時間がたつと感染から復帰します。 感染から復帰した人は、免疫を保持する除去者となりますが、時間がたつと免疫の効果が失われ感受性者の状態に戻ります。 免疫保持者がふたたび感受性者に戻るような場合は、このSIRS パターンで表すことになります。
SIR モデルにおかれていた仮定
もともとのSIR モデルは、人口の出入りのない閉じた集団における、急速かつ短期的な感染症の流行を対象にしています。 病気の流行期間が比較的短いため、出生や死亡等による人口の出入りについてあまり考える必要がなく、 人々が互いに均等に接触するような状況が想定されています。SARS、ペスト、新型インフルエンザなどのパンデミック(爆発的流行)のような現象ですね。 このような状況を想定したSIR モデルでは、基本再生産数(basic reproduction number)という数が、決定的に重要になります。 接触頻度、感染確率、感染期間をどう設定するかによって決まる数で、ひとりの感染者が何人くらいの新たな感染者を生み出すのかを示しています。 これが1より大きければ感染は住民全体に広がり、1未満であれば感染は部分的なものに止まります。 流行伝播モデルでも、この基本再生産数を計算してみることができます。流行に感染した人が、平均して何人くらいの新たな感染者を生み出しているのかを計測します。 流行伝播モデルの基本再生産数は、人口密度、移動速度、感染確率や感染期間によって左右されます。ただ、SIR モデルのように、 設定するのではなく、住民のおかれた状況により感染過程のなかで刻々と変動するのが面白いところです。
もともとのSIR モデルで置かれていた、
○住民は、他地域の住民と交流せず、出生や自然死によるメンバーの出入りもない。
○住民は、十分に混ざって生活していて均等に交流している。
○感染率、免疫獲得率、死亡率などは均質で不変である。
といった仮定は、場合によっては不自然すぎることがあります。 感染症が流行している地域と流行していない地域が生じることもあるでしょうし、長期間の感染症の流行を考えようと思えば、 出生により新たな感受性者の人口増加もあるでしょう。 もちろん、この制約を乗り越えるために、さまざまに工夫をこらした研究がされているわけですが、エージェントベースモデルである流行伝播モデルでは、 住民間の感染過程そのものを、より具体的なかたちでモデル化しているので、複雑な状況も簡単に組み込むことができるという特長を持ちます。
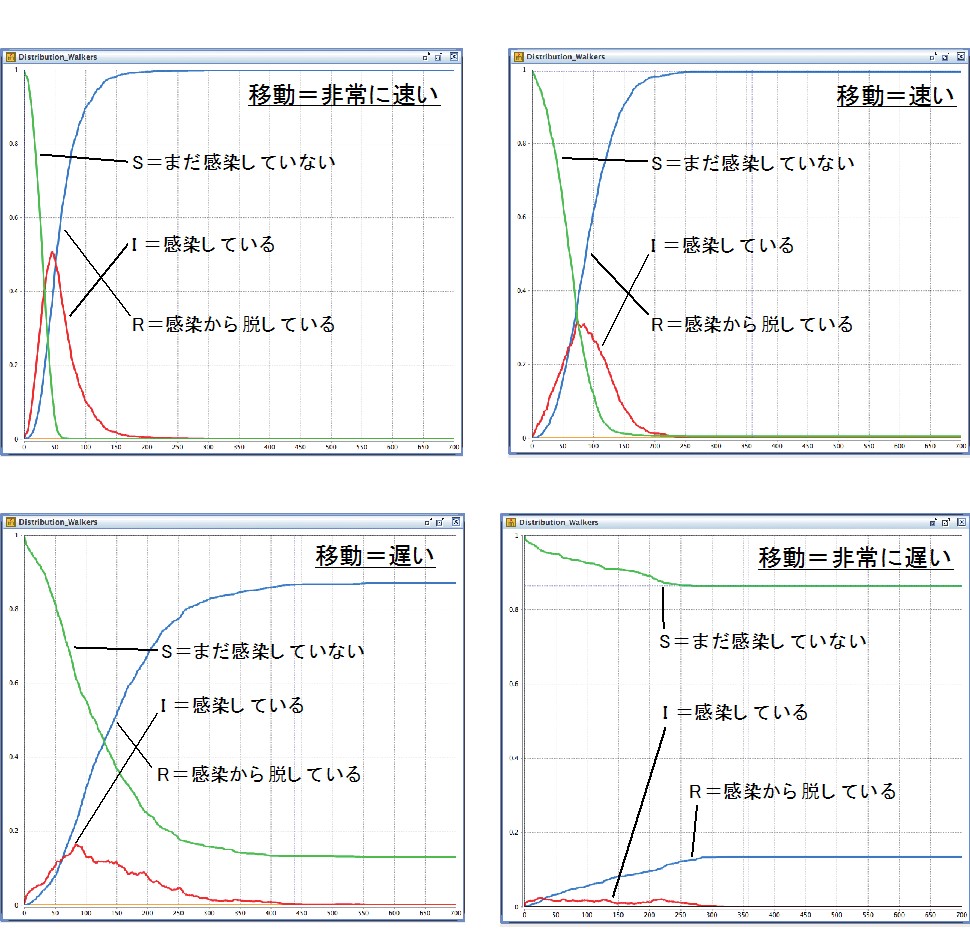
たとえば、流行伝播モデル(SIR パターン)における、人々の移動速度を変えてみましょう。 移動速度が速い場合、人々は十分に混ざって生活していることになり、均等に交流している状況になります。 逆に移動速度が遅い場合は、人々のうごきは不活発で、人々はあまり混ざらずに生活していることになります。 それぞれの場合で、流行伝播の状況は大きく異なります(下図参照)。 人々の移動速度が速い場合は、流行は全体に広がりますが、人々の移動速度が遅い場合は、流行は全体に広がることなく収まります。 注目すべき点は、いずれの場合でも、上述した基本再生産数(basic reproduction number)は(大きく変動しつつも)、同じくらいの値だということです。 基本再生産数が同じ、つまり流行に感染した人がおおよそ同じくらいの数の新たな感染者を生み出す状況でも、 人々の交流が均等に行われているか、住民がよく接触する隣人とあまりしない他人をもつといったかたちで、交流が不均等であるか、によって流行現象に大きな違いが生じることが分かります。
ほかの流行現象への応用の可能性
SIR モデルおよび流行伝播モデルの発想は、病気だけでなく、噂や情報の伝播や新製品やファッションの流行など、 さまざまなものの流行伝播の社会現象についてのモデルとして応用することができます。
感染者(I)に感染力のある期間が設定されていることは、新しい情報(噂や新製品)について「せっかく知ったことだからできるだけ早く多くの友達に伝えたい」と考えるが、 時間が経つと「もう古い情報だから人に言ってもしょうがない」と考え直す人々の性向を表しているととらえることができます。 除去者(R)は、流行に反する者の社会からの排除と捉えることもできるし、流行に従った者が転向により流行から外れたことなどを表すことができます。 ただ単に新しい情報(噂や新製品)を忘却してしまう場合は、除去者ではなく、ふたたび感受性者(S)に戻るSIS モデルで表すことができます。 最初に新しい情報に接触しただけでは消化しきれず、次の人に伝達するまでに時間的猶予が必要であったり、 態度変更までに時間的な遅れが存在したりする場合には、潜伏感染者(E)として表されることになります。 いったん購入した製品を短期間で買いかえることのない耐久財の場合は、SI モデルで表すことができます。
このように、SIR モデルおよび流行伝播モデルは、普遍的な現象を簡素な仕組みでとらえることが可能であり、工夫を加えることで、 さまざまなパターンの流行現象にあてはめる可能性を持っています。
もっと読むなら
W. O. Kermack and A. G. Mckendrick (1927) “A Contribution to the Mathematical Theory of Epidemics Part !,” Proceedings of Royal Society, series A, vol.115, pp.700-721.
佐藤総夫(1987)『自然の数理と社会の数理:微分方程式で解析するII』日本評論社
キーワード:感染症・伝染病・流行・伝播・SIR モデル・マルチエージェント・シミュレーション・モデル
|
流行伝播モデル 基本情報 【モデルタイトル】:流行伝播モデル(Diffusion Model) artisoc Cloud artisoc4【モデル考案者】:光辻克馬 【モデル発表年】:2018 【サンプルモデル作成者】:光辻克馬 【説明文文責】:光辻克馬(東京大学) |
