MASのモデル
砂山くずしモデル
砂山くずしのモデルは大災害のモデル
砂山くずし(sand-pile)のモデルは、デンマークの物理学者パー・バックらによって1987年に発表された数理モデルです。開発者3人(Per Bak、Chao Tang、Kurt Wiesenfeld)の名前の頭文字をとってBTWモデルとも言われます。
砂山くずしのモデルという名前ですが、中身はブロックくずしになっています。実際の砂山はさらさらしすぎていて、BTWモデルと同じ性質を示さないそうです。砂山くずしのモデルは、地震や大火災や恐慌といった大災害が起こる仕組みを私たちに教えてくれます。
砂山くずしのモデルは、大災害が何でもないようなルールから生じることを示しており、その何でもないルールが、大災害のような稀に起こる大規模な現象と同時に、ふだんから起こる普通の現象も同じように起こすことも教えてくれます。バックらは、この仕組みを「自己組織化臨界(self-organized criticality)」と名付けました。

砂山くずしモデルのルール
砂山くずしのモデルは、マス目の広がっている空間にブロックが落ちてきて積まれていくモデルです。
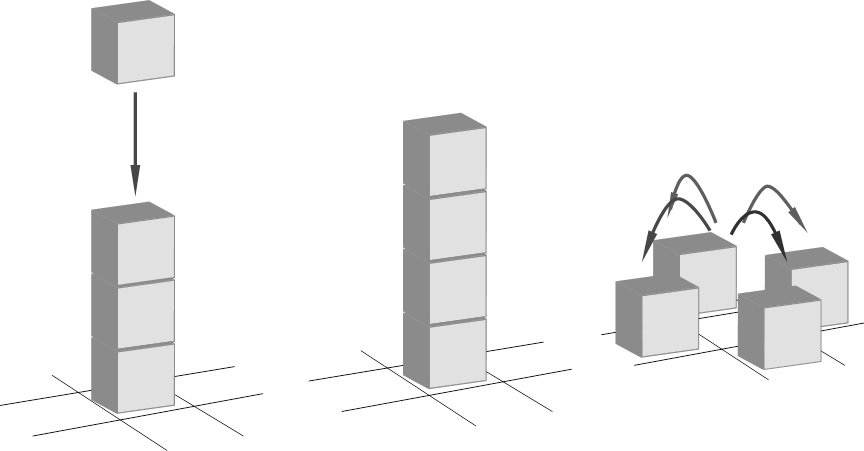
毎回、空間のなかから1つのマス目が選ばれ、そこに1つのブロックが積まれます。すでにブロックのあるマス目にブロックが落ちてくると、すでにあるブロックの上にブロックが積まれていきます。
ただし、1つのマス目に4つのブロックが積まれると、その4つのブロックは、周囲の4つのマス目に飛散します。そのマス目にすでに3つのブロックが積まれていた場合、マス目にあるブロックは4つになり、そこからさらに飛散が起こります。
飛散の連鎖は、どのマス目にも4つのブロックがなくなるまで続きます。連鎖が全く起こらないこともあれば、長く連鎖が続くこともあります。
砂山くずしモデルの何が面白いの?
ブロックの飛散によって起こるなだれは、連鎖して大規模になる場合と、連鎖せずに小規模でおさまる場合があります。
もちろん大規模な連鎖はあまり起こらず、小規模な連鎖はよく起こります。
そして、興味深いことに、なだれの規模と頻度のあいだには、「べき乗則」と言われる一定の法則性が見られるのです。
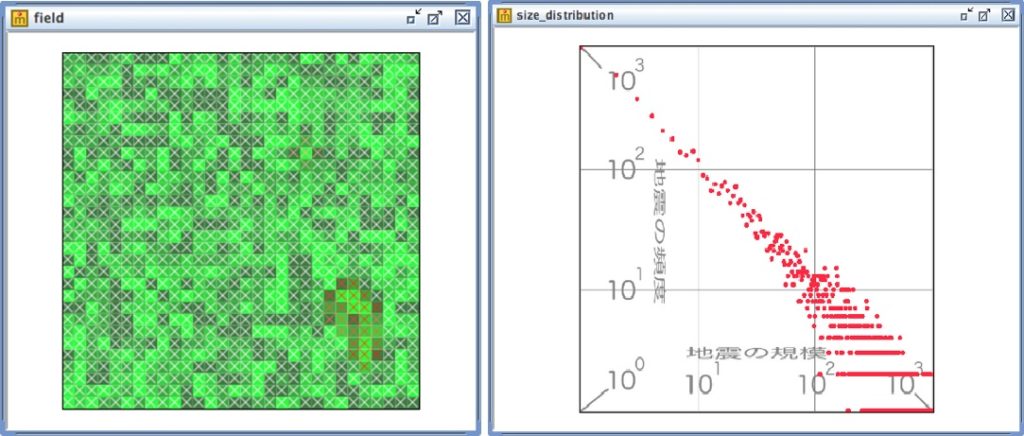
べき乗則について、そのなかでも、もっとも簡単なべき乗則であるジップの法則を使って説明します。出来事の規模(10a)と頻度(10b)を測ったとき、a+bが常に一定の値になるというのがジップの法則です。
この法則にもとづいている現象では、大規模な出来事の起こる頻度は低く、小規模な出来事の起こる頻度は高いのですが(まあこれはそんな不思議じゃないですね)、大規模な出来事の起こる頻度がそこまで低いわけではなく、小規模な出来事の起こる頻度がとっても高いという特徴をもちます。
ある現象の規模がべき乗則を示すということは、とても大規模な出来事も低いながらもそこそこの頻度で起こり、とても小規模な出来事が想像以上の高い頻度で起こっていることを意味しているのです。
べき乗則(ジップの法則)にもとづいている現象では、これまで起こった現象の規模の平均値をとると、測り方によってその結果は大きく変動してしまいます。そのため、べき乗則にもとづいて起こる現象については、これまで起こったことの平均値をもとに、未来の出来事の規模を推定することが実はできません。期待値を計算して、これから起こるであろう現象の規模を予測しようとすると、その結果は発散してしまい(分母も分子も無限大になってしまう)、計算できないといったことが起こってしまうのです。
これは、その系で、あらゆる規模の出来事が起こりうる性質を持っていることを示しており、ちょっとした変化により、全く異なった質のものに変わってしまう(相転移といいます)際(きわ)にあることを意味しています。このことを、その系が臨界状態にあるといいます。
地震や火災、恐慌や戦争などの災害には、べき乗則が見られると考えられています。べき乗則は、これら大災害だけでなく、都市の規模や知り合いの数、本・音楽の売り上げ、ウェブサイトのヒット数、会社の規模や土地の値段、生物の種類ごとの数や月のクレーターの大きさなど、さまざまなものの中に観察されると考えられている法則性です。
ップの法則は、1930年代初めにジップ(George Kingsley ZIPF)によって提唱された法則で、べき乗則のひとつにあたります。ジップはなんとの文章のなかの単語の使用頻度に、この法則性を見つけたのです。
BTWの砂山くずしモデルは、このべき乗則を示す臨界状態の背後にあるメカニズムを説明するための大きなヒントを示していると考えられています。
森林火災モデル:BTWモデルの簡易版
BTWの砂山くずしモデルは、地震の起こる仕組みをイメージして考えられたモデルです。これをもう少し簡素な仕組みにして、火災を起こる仕組みにあてはめた森林火災のモデルがあります。
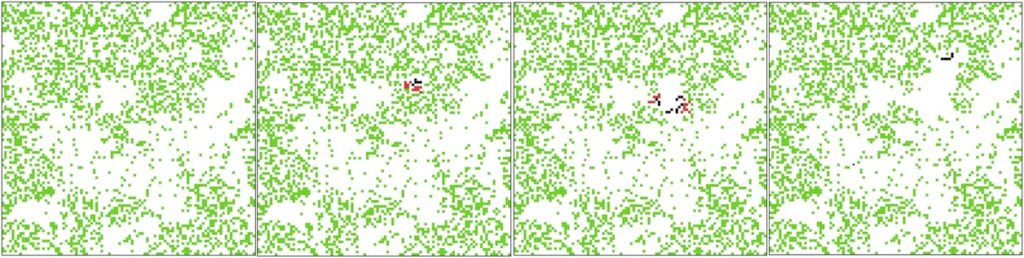
森林火災モデルの基本は、空間にしきつめられている木があって、となりに燃えている木があると自分も燃えてしまうというものです。燃えた木はしばらくすると燃え尽きて消滅してしまいます。
森林火災モデルで、いつも無作為に選ばれた空き地に木が生えてくることにします。一方で、ときどき無作為に選ばれた場所で火災が起こるものとします。木が自然に生えてくるので、森林の樹木密度は増えていきます。一方で、ときどき起こる火災によって樹木密度は減ることになります。
自己組織化臨界版の森林火災モデルで、森林火災の多くは小規模なものですが、ときどき、とてつもなく大きな火災が起こることになります。そして、この森林火災の規模と頻度が、やはりべき乗則に従うことが知られているのです。
「つりあい」ではなく「せめぎあい」:自己組織化臨界
砂山くずしのモデルが提唱した自己組織化臨界という考え方は、世界についての新しい見方を提案しています。
べき乗則が見られる臨界状態では、落石から大雪崩まで、ボヤから大火災まで、あらゆる規模の現象が起こる状態になっています。そして、相互作用のある大規模な系が、自然に(勝手に/自己組織的に)臨界状態に向かい、その状態を保つ性質をもつことを砂山くずしのモデルは示しています。
砂山くずしのモデルでは、ブロックが落ちてくるルールが系のなかにあるブロックを徐々に増やし、ブロックが飛散するルールがブロックを系の外に弾いて減らそうとしています。
森林火災のモデルでは、樹木の成長が系のなかにある樹木を増やし、火災が樹木を減らそうとしています。これらの2つの力の「せめぎあい」が系を臨界状態へと移行させています。
世界にある多くのものは、相互作用のある大規模な系としての性質を持ちます。そして、べき乗則という規則性がさまざまな現象に見られることは、それらの大きな系は、臨界状態へと自然に向かう性質を持っており、世界に存在している多くのものは、実際にその状態にあると考えられるのかもしれません。
たとえば経済学では、市場経済の性質を、価格をめぐるさまざまな力の均衡(「つりあい」)として理解するように教えています。もしそれが正しいのならば、不況や大恐慌といった大変動は、それを引き起こす別の大きな理由や要因があるはずです。
しかし、市場経済を、力の「せめぎあい」の起こる自己組織化臨界として理解すれば(・・例えば、価格を上げる力と下げる力、企業を創る力と壊す力のせめぎあいというふうに・・)、価格の暴落や恐慌が起こることは市場そのものがもつ性質であると理解できることになるでしょう。
もっと読むなら
Per BAK, Chao TANG and Kurt WIESENFELD, 1988, “Self-Organized Criticality,” Physical Review A, Vol.38, No.1, pp.364-374.
香取眞理(1997)『複雑系を解く確率モデル:こんな秩序が自然を操る』講談社ブルーバックス(B1189)第4章
マーク・ブキャナン[水谷淳訳](2009)『歴史は「べき乗則」で動く:種の絶滅から戦争までを読み解く複雑系科学』早川書房[早川文庫]
キーワード:砂山くずし,自己組織化臨界現象,BTWモデル,Sand-Pileモデル,森林火災,マルチエージェント・シミュレーション・モデル
|
砂山くずしモデル 基本情報 【モデルタイトル】:砂山くずしモデル artisoc Cloud artisoc4【モデル考案者】:Per BAK, Chao TANG, Kurt WIESENFELD 【モデル発表年】:1987 【artisocサンプルモデル作成者】:光辻克馬 【artisocサンプルモデル作成年】:2017 |
