MASのモデル
ライフゲームモデル
ライフゲームとは
ライフゲームとは、セルオートマトンの一種で、1970年に英国の数学者ジョン・コーンウェイ(John Conway)が考案しました。 「セルオートマトン(Cellular Automaton)」というのは、空間に格子状に敷き詰められた多数のセルが、 近隣のセルと相互作用をする中で自らの状態を時間的に変化させていく、仮想的な「自動機械(オートマトン)」のことです(⇒<セルオートマトンモデル>を参照)。
ごく抽象的なモデルですが、様々な物理現象や生命現象の本質を表現できるモデルとして、単純なものから複雑なものまでいろいろな種類のセルオートマトンが考案されてきました。 ライフゲームも直接的には生命現象をモデル化するために作られました。 自己増殖など、生命体が示すような複雑なダイナミクスを、ごく単純な規則から生み出すことができます。 実際、個々のセルが変化する中で実に様々なパターンが空間上に現れるため、それらが生命現象であるかどうかは別にして、単純に見ていて飽きることがありません。 そのため、ライフゲームは、研究者のみならず、様々な人々の興味・関心・趣味の対象となってきました。おそらく最も有名なセルオートマトンと言えるのではないでしょうか。

モデルのルール
コーンウェイは、できるだけ単純な規則からできるだけ複雑な現象を生み出すことに腐心して、ライフゲームに行き着いたと言われています。そのため、そのルールはとても単純です。
最初に、二次元空間にセル—文字通り「細胞」の意味で捉えてもいいかもしれません—が敷き詰められている状況を想定します。 各セルは二つの状態を持っていて、各時点いずれかの状態を取っているものとします。ここでは、二つの状態が「生」「死」を表していると考えましょう。 時間は1ステップ刻みで流れていて、各セルの次のステップの状態は、現ステップの自身の状態と隣接する周囲八つのセル—これを「ムーア近傍」と言います—の状態で決まります(下図参照)。 具体的には以下のようなルールが適用されます。
・誕生:現ステップ「死」のセルの近傍に「生」のセルがちょうど三つあれば、中心のセルの次ステップの状態は「生」になる。
・生存:現ステップ「生」のセルの近傍に「生」のセルが二つか三つあれば、中心のセルの次ステップの状態は「生」のままである。
・過疎:現ステップ「生」のセルの近傍に「生」のセルが一つ以下しかなければ、中心のセルの次ステップの状態は「死」になる。
・過密:現ステップ「生」のセルの近傍に「生」のセルが四つ以上あれば、中心のセルの次ステップの状態は「死」になる。

ムーア近傍:中心セルの次期の状態は今期の自身と近傍の状態から決まる
これは他のセルオートマトンのモデルにも言えることですが、各セルの状態の変化の仕方を定める上記のルールには、全くランダムな要素がなく、その意味で完全に決定論的です。 しかし、このルールを適用し始める前に空間上のセルが取りうる「生」と「死」の状態の組み合わせ—つまり「初期状態」—は、際限なく考えられます。 たとえば、空間の大きさを50×50に限定したとしても、この組み合わせの数は2の2500乗になります。これはとてつもなく大きな数です。 こうした無数の初期状態の一つ一つに、上記の単純なルールを逐次的に適用していくことで、驚くほど豊かな「ライフゲームの宇宙」が展開されることになるのです。
サンプルモデルの操作方法
サンプルモデルでは、このようなライフゲームの豊かなダイナミクスをartisoc Cloud上で手軽に観察することができます。 コントロールパネルの「配置」で初期状態を指定し、あとは実行ボタンを押すだけです。
「配置」で「random」を選ぶと、ランダムな初期状態が生成されます。この場合、一定の割合のセルが無作為に選ばれ、各々の状態が「生」になります。 なお、画面上で「生」は赤色、「死」は水色で表示されます。
「配置」で「random」以外、たとえば「glider」や「Gosper_glider_gun」を選ぶと、ライフゲームの研究者やファンの間でよく知られた特定の初期状態から始めることができます。 「glider(グライダー)」から始めると、一群の「生」のセルが、状態変化のルールにしたがって一定方向に伝播し続ける結果、さもグライダーが空を飛び続けるかのようなダイナミクスを観察することができます。 また、「Gosper_glider_gun(ゴスパーのグライダー銃)」から始めると、このグライダーが延々と連続発射されていく、より複雑なパターンを観察することができます。
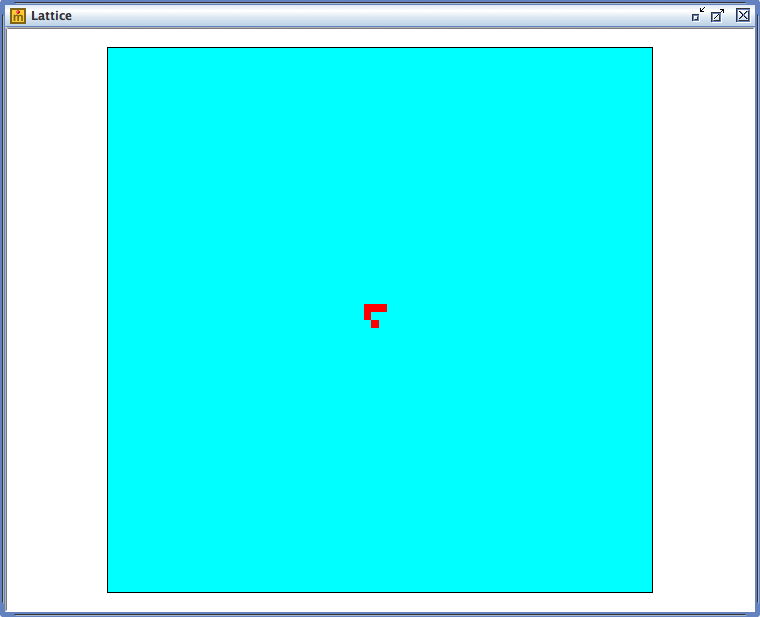
「グライダー(glider)」の初期状態
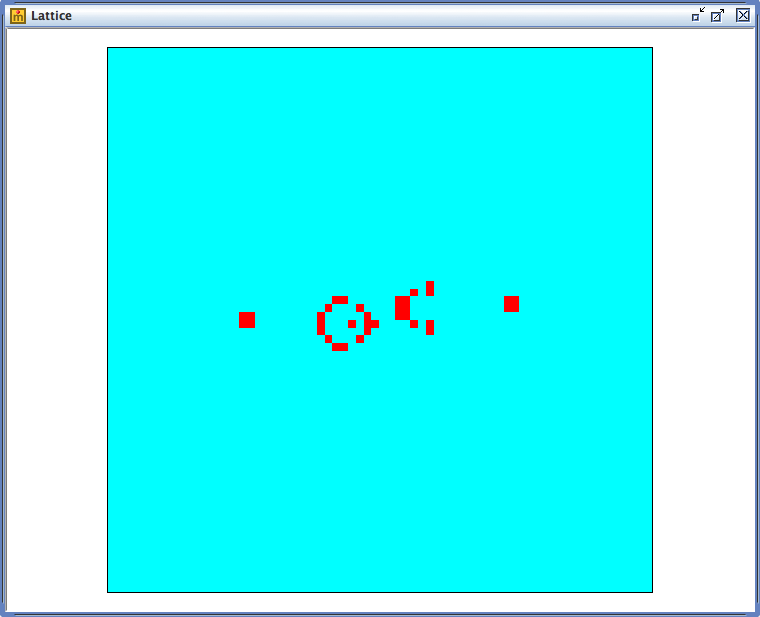
「ゴスパーのグライダー銃(Gosper_glider_gun)」の初期状態
これらのパターンは大変よく知られたものですので、インターネットを調べれば、たいてい情報を得ることができるはずです(たとえばWikipediaなど)。
より進んだ操作方法
「Life Lexicon」というサイト(英語)(⇒こちら)では、 これまでに「発見」された膨大な数のライフゲームの初期状態が、アルファベット順にカタログ化され紹介されています。 実は、サンプルモデルでは、この「Life Lexicon」から好みの初期状態のデータをダウンロードして、articos上に読み込むことができます。 やり方は以下のように簡単ですので、ぜひ試してみてください。
・「Life Lexicon」で、入手したい初期状態(たとえば「bakery」)の画像アイコンをクリックして、初期状態のデータファイル(「bakery.cell」)をダウンロードします。
・入力ファイルの「configs.zip」をダウンロードし、データファイルを入れてzipファイルを作成し、アップロードします。
・コントロールパネルの設定で「配置」を選択して「リスト項目」の文字列に「,"bakery"」を追加すると、データファイルを選択できるようになります。
・もし、「Life Lexicon」で入手した初期状態の配置に要するスペースが、サンプルモデルの空間の大きさを超える場合は、実行ボタンを押した途端にエラーが起きてしまいます。 その場合は、空間サイズを拡大するなどの対応を行いましょう。
モデルの見どころ
ライフゲームは、多くの要素の間の単純な局所的相互作用から、多様で複雑な大域的振る舞いがもたらされる、複雑系のエッセンスを凝縮したようなモデルです。 様々な初期状態から生まれるこうした振る舞いを、できるだけたくさん見て楽しんでもらいたいと思います。 ライフゲームが示すパターンやダイナミクスについては、確立された類型がある訳ではありませんが、たとえばWikipedia日本語版では、以下のような分類が示されています
・固定物体:セルの状態がいつまでも変化しないもの(サンプルモデルでは「Mickey_Mouse」)
・振動子:一定の周期で同じパターンに戻るもの(「Koks_galaxy」「Pentadecathlon」)
・移動物体:一定のパターンを繰り返しながら移動していくもの(「big_glider」「glider」「lightweight_spaceship」「heavyweight_spaceship」)
・繁殖型:(空間が無限に広がっていれば)無限に増殖を続けるもの(「Gosper_glider_gun」「puffer_train」)
・長寿型(メトセラ):長い世代(場合によっては何万世代)にわたって不規則な変化を続けるもの(「acorn」「diehard」「R-pentomino」)
実は、こうしたパターンの背後には、物理、生命、情報処理などに関わる深遠な原理が潜んでいると言われています。 ライフゲームのよりディープな世界に関心がある人は、「もっと読むなら」に挙げた本を読んでみるといいでしょう。
もっと読むなら
・Levy, Steven(服部桂訳). 1996. 『人工生命: デジタル生物の創造者たち』朝日新聞社.
・William Poundstone(有澤誠訳).2003.『ライフゲイムの宇宙』日本評論社.
|
ライフゲームモデル 基本情報 【モデルタイトル】:ライフゲームモデル artisoc Cloud artisoc4【モデル考案者】:John Conway 【モデル発表年】:1970 【サンプルモデル作成者】:阪本拓人(東京大学) 【説明文文責】:阪本拓人(東京大学) |
