MASのモデル
セルオートマトンモデル
基本セルオートマトンとは
セルオートマトン(Cellular Automaton, CA)とは、空間に格子状に敷き詰められた多数のセルが、近隣のセルと相互作用をする中で自らの状態を時間的に変化させていく「自動機械(オートマトン)」です。各セルの状態が離散的な値(「0」「1」「2」など)を取る点、各セルは周囲一定範囲内(近傍)のセルと局所的な相互作用を行う点、次期のセルの状態は自身と近傍のセルの今期の状態から決定論的に決められる点などが特徴です。このようにCAは抽象的なモデルですが、様々な物理現象や生命現象のエッセンスを捉えたモデルとして古くから研究されてきました。たとえば、乱流、結晶の成長や細胞の自己増殖といった現象が、CAを使ってモデル化できます。また、セルの値の並び(「01000101…」など)が、計算機が処理するデータやプログラムを表していると考えると、CAは単純で抽象化された計算機のモデルにもなります。よく知られているCAとして、二次元空間上で展開するコンウェイの「ライフ・ゲーム(Game of Life)」が有名です。 (⇒ライフゲームモデルを参照)。

ここで取り上げる基本セルオートマトン(Elementary Cellular Automaton, ECA)は、このようなCAの中でも最も単純な部類に属するモデルです。セルは1次元空間(つまり直線上)に並んでいて、各々が取りうる状態は2つのみです。またそれぞれのセルは、両隣のセルとしか相互作用しません。まさに基本中の基本のセルオートマトンです。ECAはその単純な構造ゆえに、セルの状態変化を決めるルール(変化規則)を網羅的に調べ上げることができます。実際に、1980年代にスティーブン・ウルフラム(Stephen Wolfram)という理論物理学者が、「複雑系」「自己組織化」といった観点から、そのような研究を行っています。彼の研究によって、いくつかのECAのルールから、複雑な構造を伴った、興味深い大域的な振る舞いがもたらされることが分かっています。
モデルのルール
ECAのルールはごく簡単です。いま、ある数(サンプルモデルでは300個)のセルが一直線上に並んでいます(空間がループしているので厳密には環状につながっています)。各セルは「1」か「0」の二つの状態を持つものとします。サンプルモデルのマップ出力では「1」が青、「0」が白で表されています。
各セルの状態は、左右二つのセルの状態と自らの状態、つまり隣接する三つのセルの状態の組み合わせに応じて変化していきます。このような組み合わせは、2×2×2=8通りあります。たとえば以下のように(網掛け部は規則が適用されるセル)、8つの場合各々についてセルが次時点で「1」「0」いずれの状態を取るかを決めることで、セルの変化規則が定義されることになります。

このような規則を各セルに反復して適用したときに、セルの並び全体がどのように変化していくのかを見るのがモデルの主眼です。モデルの出力のうち「State Transition(状態遷移)」は、各時点におけるセルの並びの状態を、縦軸を時間軸として二次元空間にプロットしていったものです。セルの並びの複雑な変化の様子がグラフィカルに表現されます。
サンプルモデルの操作方法
三つのセルの状態の組み合わせ8通りに対して、「1」「0」いずれかを指定することでセルの変化規則が定まります。このような変化規則は論理的には28=256通り存在し、コントロールパネルを操作することでこれらの規則を指定することができます。たとえば「101」のスライドバーを「1」にすると、左右のセルが「1」で真ん中のセルが「0」の場合、次の時点の真ん中のセルの状態は「1」に変化することになります。
ところで、このようにして8通りの状態に対応する8つの数字を指定すると、一つの変化規則は8桁の二進数で表現できます。たとえば、先述の変化規則のように、「000」に対して「0」、「001」に対して「1」、「010」に対して「1」、…「111」に対して「0」という具合に指定すると、この変化規則は(右から数字を並べていき)「00001110」という二進数で完全に記述できます。これを十進数に変換すると14(21×1+22×1+23×1)です。サンプルモデルでは、コントロールパネルの「Decimal」をオンにして、スライドバー「RuleNumber」で0〜255の範囲の整数値を一つ選ぶことで、このような十進数(「ウルフラム・コード」と呼ぶこともあります)によるルール指定も行うことができます。
また、初期時点でのセルの状態も変化させることができます。コントロールパネルの「RandomConfig」のボタンをオンにし、スライドバー「InitDensity」で「1」のセルの比率を操作することで、 様々な初期状態をランダムに生成することができます。一方、「RandomConfig」のボタンをオフにすると、真ん中のセルのみが「1」の初期状態から始めることができます。
様々な規則と様々な初期状態を組み合わせて、どのような秩序が生成されてくるかを観察してみましょう。
モデルの見どころ
ウルフラムは、ECAの大域的な振る舞いを四つのクラスに分類しています。
クラス1は、どのような初期状態から始めても、やがて全てのセルが均質な状態(全てのセルの状態が「1」になるなど)になるパターンで、状態遷移の出力としてはたとえば以下の画面のようになります(十進数によるルール番号は248で、2進数で表すと「11111000」)。

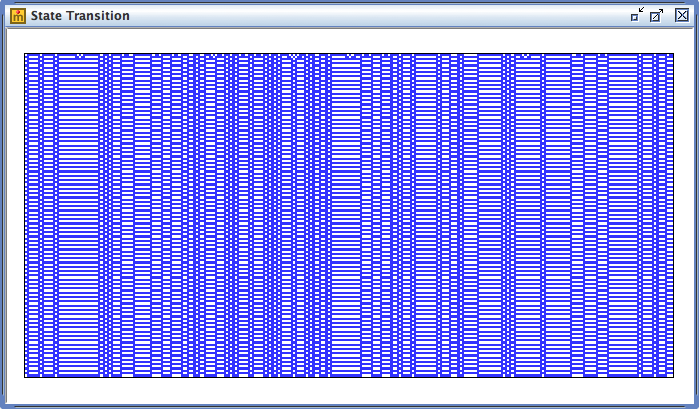
クラス2は、セルがやがていくつかの均質な状態の局所的な集合に分かれたり、周期的な状態変化を繰り返したりするパターンで、クラス1と同様に安定性の高いパターンと考えられています。以下の画面がクラス2の例になります(ルール番号は123、二進数表記で「01111011」)。
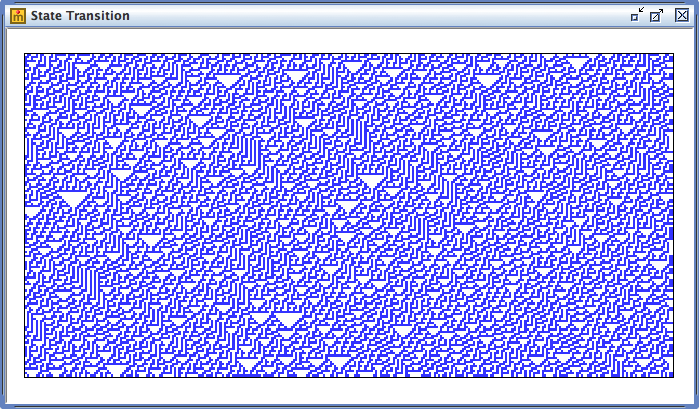
クラス3はカオス的なパターンであり、以下の画面のように、乱雑な変化の中に自己相似的な局所構造(以下の例では逆三角形)が現れることもあります。この例はルール番号30(二進数表記で「00011110」)をランダムな初期状態に適用したものですが、イモガイなどの貝の貝殻の模様と酷似しているということで注目を集めました。
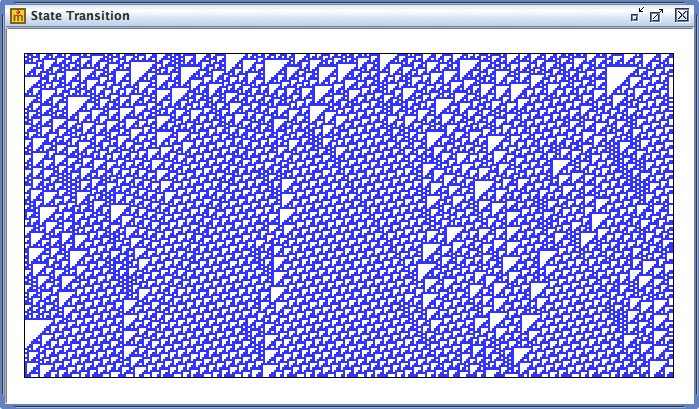
最後にクラス4は、クラス1・2の秩序状態とクラス3のカオス状態が共存するような複雑な大域的状態に至るパターンです。クラス4の挙動を示す変化規則として知られているのは、ルール番号110(二進数表記で「01101110」)であり、下図はこのルールをランダムな初期状態に適用した際の状態遷移を表しています。ルール110は、いわゆる「万能計算(universal computation)」を行えることが証明されていて、非常に複雑な情報処理ができることが知られています。
もっと読むなら
Levy, Steven(服部桂訳). 1996. 『人工生命: デジタル生物の創造者たち』朝日新聞社.
Schiff, Joel L.(梅尾他訳). 2011. 『セルオートマトン』共立出版.
Wolfram, Stephen. 1994. Cellular Automata and Complexity: Collected Papers. Reading, Mass.: Addison-Wesley Pub. Co. Mitchell, Melanie, Tino Gramß, Stefan Bornholdt, Michael Groß, Melanie Mitchell, and Thomas Pellizzari. 2005.
"Computation in Cellular Automata: A Selected Review." In Non-Standard Computation, 95-140. Wiley-VCH Verlag GmbH & Co. KGaA.
|
基本セルオートマトンモデル 基本情報 【モデルタイトル】:基本セルオートマトンモデル artisoc Cloud artisoc4【モデル考案者】:Stephen Wolfram 【artisocサンプルモデル作成】:阪本拓人 【artisocサンプルモデル作成日】:2017年7月11日 |
