MASのモデル
バラバシ・アルバートモデル
バラバシ・アルバートモデルとは
ネットワークにおいて、一部のノード(要素)が膨大なリンク(つながり)を持つ一方で、ほとんどのノードはごくわずかなノードとしかつながっていないような ネットワーク構造をスケールフリー ネットワークと言います。
スケールフリーネットワークは、航空機の路線や電力網、学術論文の引用関係、WEBのリンク関係など社会のいたるところで観察されます。
1999年に、バラバシと彼の学生のアルバートが、それなりに現実らしい作り方でスケールフリー性が実現されるネットワークのモデル(BAモデル)を提案しました。
BAモデルの2つの特徴は「ネットワークの成長」と「優先的選択」です。
ノードを次々とネットワークに加え(成長)、新しく加えたノードを元から存在するどのノードと結びつくかを等確率で選択した場合、スケールフリーになりません。 BAモデルでは、その時点で次数の高いノードに結びつきやすくする(優先的選択)ことにより、次数が高くなった頂点は、その後も新しいリンクを獲得しやすくなり、ハブになりやすいというスケールフリー性を実現します。
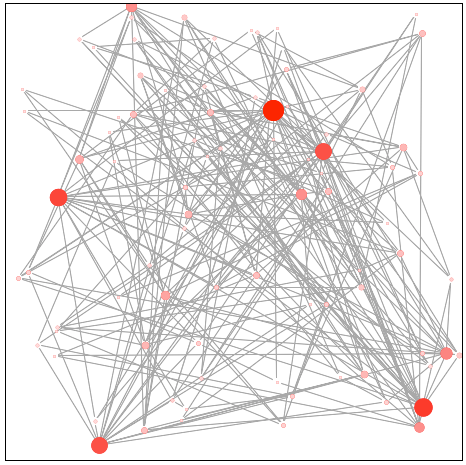
スケールフリー・ネットワークを再現
スケールフリー・ネットワークができるまでの様子をシミュレーションで見てみましょう。
バラバシ・アルバートモデルのルールとして以下のように定義します。
①1つのノード(もしくは相互に繋がったいくつかのノード)からスタートとします。
② 新しいノードを追加します。このノードから、すでに存在しているノードに対してリンクを張ります。このとき、リンクが張られる確率は、それぞれのノードのその時点でのリンク数に比例するものとします。
③ ②をノードが所定の数になるまで繰り返します。
上記モデルでスケールフリーネットワークができる過程をシミュレーションしてみます。
モデルの面白いところ
・「ハブ」の存在
ずば抜けて多くのリンクを持つノードを「ハブ」と呼びます。人気ブロガーがおすすめした商品がブレークしたり、噂が一気に拡散したり、「ハブ」の影響力は絶大です。
・べき法則
リンク数と同じリンク数を持つノードの数の度数分布を両対数グラフで表すと右下がりの直線になることを「べき法則」に従うと言います。地震の大きさと発生回数もべき法則に近い関係にあります。
・スケールフリー・ネットワーク
ごく少数のノードが莫大なリンクを持ち、大半のノードがごく少数のリンクしか持たないネットワーク構造を「スケールフリー・ネットワーク」と呼びます。一方、どのノードも同じくらいの数のリンクを持つネットワーク構造を「ランダム・ネットワーク」と呼びます。
もっと読むなら
[1] Barabasi, A.-L., and Albert, R., Emergence of scaling in random networks, Science 286, 1999, pp. 509-512.
[2] Albert-laszlo Barabasi, Jennifer Frangos, Linked: The New Science Of Networks Science Of Networks, Basic Books (2002/5/14), ISBN 0738206679
[3] アルバート=ラズロ・バラバシ, 青木薫(訳), 『新ネットワーク思考―世界のしくみを読み解く』, NHK出版, 2002年12月, ISBN 4-14-080743-1
[4] 増田直紀, 今野紀雄, 『複雑ネットワーク―基礎から応用まで』, 近代科学社, 2010年4月, ISBN 978-4-7649-0363-0
|
バラバシ・アルバートモデル 基本情報 【モデルタイトル】:バラバシ・アルバートモデル(BAモデル) artisoc Cloud artisoc4【モデル考案者】:Barabasi, A.-L., and Albert, R. 【モデル発表年】:1999 【artisocサンプルモデル作成】:構造計画研究所 玉田正樹 【artisocサンプルモデル作成日】:2006年10月 |
