身の回りの複雑系

直感と真実｡『確率』を理解しよう!

モンティ・ホール問題をご存知でしょうか？

詳しくはこちら（ウィキペディア）に載っていますが、名前の由来は、
モンティ・ホールさんが司会をしていたアメリカのゲームショー番組の中で、ゲームの確率論に関する論争が起きたことに由来するそうです。

私もはじめ解説を読んだ時は、「1/2なのになんで？？」と思いましたが、いろいろな解説を読んでみたところ理解することができたような気がします。しかし、ルールを理解し納得できたとはいえ、腑に落ちない感じもします...。

Question

扉が閉まっているドアが３つあり、ドアの中に1つは当たりの景品の新車、２つははずれを意味するヤギがいます。プレーヤーは新車のドアを当てると新車がもらえます。

Answer

直感だと、残りは２つなのでどちらを選んでも確率は1/2だと思いませんか？
変えても変えなくても【運】次第！

しかし勝率を計算すると、プレーヤーがドアを変更しない時の当たりの確率は1/3
変更すると、2倍の2/3という値となると結果が出ました。

理論的に説明しているものを読むと、数式がたくさん出てきて難しそうです。

有名問題・定理から学ぶ数学　条件付き確率問題《モンティ・ホール問題》
https://wkmath.org/cond-prob-f.html#q-mon-hal-prob（参照 2023-03-15）

artisoc Cloudでシミュレーションしてみよう！

モンティ・ホールさんに「変更してもいいですよ」と言われ、悩んだ末 “変更する” 場合

まずは100回試してみましょう。
＜artisoc Cloudの手順＞
１．左側のコントロールパネルで「実行回数」100を選択
２．「あなたの選択」で、 ”変更する” を選択
３．開始ボタン ▶ をクリック

勝率は、1回目 65％、２回目72％、3回目64％

実行回数を1,000回にしてみたら？？

勝率64％！！

10回くらいなら自分で試してみることはできますが、勝率は60％だったり80％だったりするかもしれません。artisoc Cloudを利用して、100回、1000回とシミュレーションしてみると、勝率は 2/3（66.6％）に近い値となりました。

Oracle Crystal Ballを利用して、モンテカルロ・シミュレーションをやってみよう！

「未来を予測する」ためのツールで、Excel上で“リスク分析”を行うことができる“意思決定支援ソフトウェア”です。モンテカルロ・シミュレーション技術を使って、与えられた状況の下で起こり得る結果を予測します。

まずスプレッドシートでモデルを作成します。
（作成したモデルはここでは割愛します。）

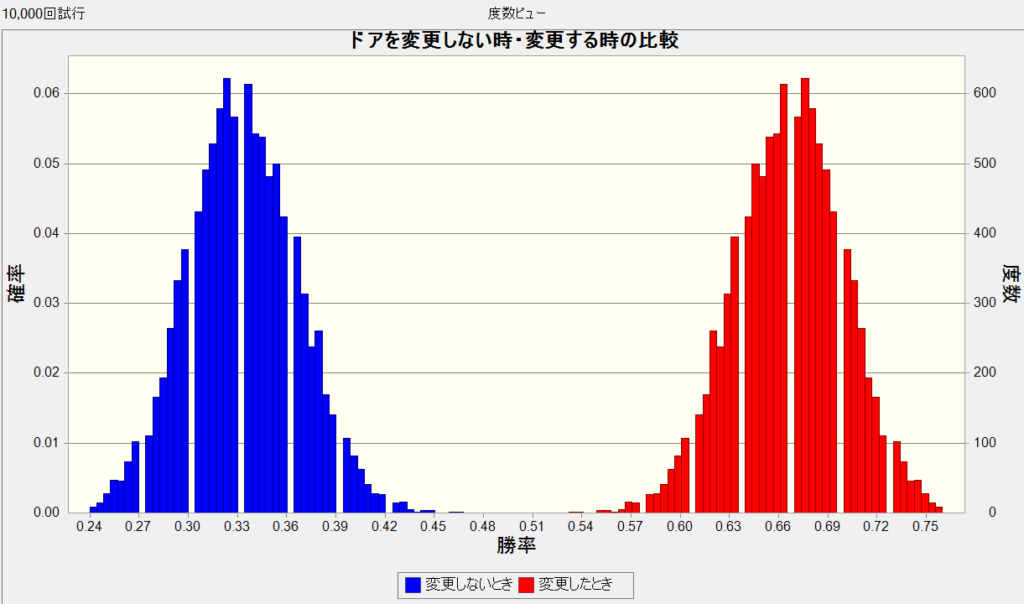
＜シミュレーションを10,000回実行した時の結果＞

ドアを変更しない時　【起こりそうな範囲：最小21%から最大47%、平均 33.3%】
ドアを変更した時　　【起こりそうな範囲：最小54%から最大80%、平均 66.6%】

1回ずつで見ると範囲の幅はありますが、平均値を見ると、勝率が2倍になることが分かりました。
シミュレーションの回数を増やすと、勝率は 2/3（66.6％）になりました。

※このモデルのシミュレーションにかかった時間は、1万回で1分弱です。
　（パソコンの性能により計算時間は変わります。）

こちらよりOracle Crystal Ball を15日間お試しいただけます。

＊＊＊

日常生活では、つい『直感』で判断しがちですが、シミュレーションを使って何千回も実験するとその中に『確率』が隠されている場合があるようです。シミュレーションを使って見えてくる『真実』があることに驚きました！

ちなみにモンティ・ホールさんはどんな方なのかと気になったので調べてみました。
https://en.wikipedia.org/wiki/Monty_Hall（ウィキペディア(英語)）

カナダでラジオやテレビ番組の司会をしており、その後アメリカに移って放送業界でキャリアを追求し、ゲーム番組の司会やプロデューサーをされていたとのことです。

（2023年3月）